the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
The Antarctic Ice Sheet response to glacial millennial-scale variability
Ilaria Tabone
Jorge Alvarez-Solas
Alexander Robinson
Marisa Montoya
The Antarctic Ice Sheet (AIS) is the largest ice sheet on Earth and hence a major potential contributor to future global sea-level rise. A wealth of studies suggest that increasing oceanic temperatures could cause a collapse of its marine-based western sector, the West Antarctic Ice Sheet, through the mechanism of marine ice-sheet instability, leading to a sea-level increase of 3–5 m. Thus, it is crucial to constrain the sensitivity of the AIS to rapid climate changes. The last glacial period is an ideal benchmark period for this purpose as it was punctuated by abrupt Dansgaard–Oeschger events at millennial timescales. Because their center of action was in the North Atlantic, where their climate impacts were largest, modeling studies have mainly focused on the millennial-scale evolution of Northern Hemisphere (NH) paleo ice sheets. Sea-level reconstructions attribute the origin of millennial-scale sea-level variations mainly to NH paleo ice sheets, with a minor but not negligible role of the AIS. Here we investigate the AIS response to millennial-scale climate variability for the first time. To this end we use a three-dimensional, thermomechanical hybrid, ice sheet–shelf model. Different oceanic sensitivities are tested and the sea-level equivalent (SLE) contributions computed. We find that whereas atmospheric variability has no appreciable effect on the AIS, changes in submarine melting rates can have a strong impact on it. We show that in contrast to the widespread assumption that the AIS is a slow reactive and static ice sheet that responds at orbital timescales only, it can lead to ice discharges of around 6 m SLE, involving substantial grounding line migrations at millennial timescales.
The Antarctic Ice Sheet (AIS) presently stores around 60 m of potential sea-level rise (Fretwell et al., 2013). It is divided into two parts, the East Antarctic Ice Sheet (EAIS) and the West Antarctic Ice Sheet (WAIS), including the Antarctic Peninsula (AP). Present-day observations show that the mass balance of the AIS is negative due to mass loss from the WAIS, whereas the EAIS maintains a positive mass balance (Martín-Español et al., 2016; Shepherd et al., 2018). Because ablation in the AIS is almost negligible except in the small region of the AP, the mechanisms that contribute to mass loss are submarine melting of floating ice shelves and calving processes at the ice front (Paolo et al., 2015; Rignot et al., 2013). The WAIS is a marine ice sheet, i.e., most of it is grounded below sea level, and it contains several large ice shelves that are thinning or calving more rapidly than the storage provided by surface accumulation. The positive mass balance of the EAIS can be explained by the fact that the amount of floating ice is considerably smaller than in the WAIS, and thus the mass loss via calving and basal melting does not surpass the accumulation.
Rising oceanic temperatures in the coming century in response to climate change can boost basal melt and reduce ice shelves. Although thinning of floating ice shelves does not directly contribute to sea-level rise, it can lead to a reduction of ice-shelf buttressing, enhancing inland ice flow as seen after the collapse of the Larsen B ice shelf (Fürst et al., 2016; Rignot et al., 2004) and Pine Island Glacier (Favier et al., 2014; Jacobs et al., 2011). In addition, most parts of the WAIS lie on a retrograde bed slope. Conceptual models suggest the existence of an inherent instability in such ice sheets, the marine ice-sheet instability (MISI; Schoof, 2007; Weertman, 1974), that could lead to a collapse of the marine grounded zones in the WAIS region. Mercer (1978) speculated about the fact that this instability could be triggered through a rise in oceanic temperatures. Collapse of the WAIS sector could cause a sea-level increase of 3–5 m (Bamber et al., 2009; Feldmann and Levermann, 2015; Sutter et al., 2016), with major implications for coastal zones (Nicholls and Cazenave, 2010). From a modeling perspective, projections differ considerably in future sea-level contributions depending on the model used and the process parameterizations therein (Bakker et al., 2017a, b; DeConto and Pollard, 2016; Golledge et al., 2015).
Improving our understanding of the AIS sensitivity is thus essential to constrain future projections (Bakker et al., 2017a). Some of the most remarkable abrupt climate changes of the near past are those of the last glacial period (LGP; 110–10 ka). Thus, one way to gain insight in this respect is to assess the response of the AIS to these past rapid climate changes. In addition, understanding the AIS behavior during these millennial-scale abrupt events will help in identifying the ultimate causes of the Dansgaard–Oeschger (DO) events. Ice-core records from the Greenland Ice Sheet (GrIS) during the LGP show the characteristic signal of DO events: a rapid warming of more than 10 K on decadal timescales followed by a slow cooling that can last from several centuries to thousands of years (e.g., Dansgaard et al., 1993). Modeling studies (e.g., Ganopolski and Rahmstorf, 2001; Rahmstorf, 2002; Shaffer et al., 2004) and reconstructions (Barker et al., 2015; Böhm et al., 2015; Henry et al., 2016; McManus et al., 2004) support the hypothesis that DO events were caused by reorganizations of the Atlantic Meridional Overturning Circulation (AMOC), with enhanced (reduced) North Atlantic Deep Water (NADW) formation during interstadials (stadials) transporting more (less) heat into high northern latitudes. In addition, marine sediment records across large areas of the North Atlantic show quasi-periodic deposition of ice-rafted detritus (IRD) (Hemming, 2004) known as Heinrich (H) events. H events are thought to have been caused by massive iceberg discharges from the paleo Laurentide Ice Sheet (LIS), possibly in response to reductions in NADW formation that, through positive feedbacks, resulted in the collapse of the AMOC (Alvarez-Solas et al., 2011, 2013; Marcott et al., 2013).
Compared to ice-core records in the GrIS, AIS ice-core records show a more gradual and symmetric sawtooth-like signal throughout the whole LGP. An increase in surface air temperature (SAT) is observed during Greenland stadials, most notably during Heinrich stadials, with cooling during interstadials. The amplitude of this signal can reach up to 2 K (Augustin et al., 2004; Petit et al., 1999; Ruth et al., 2007) and the peaks of the sawtooth signal are known as Antarctic isotope maxima (AIM). This bipolar seesaw behavior between Greenland and Antarctica is now well established (Blunier and Brook, 2001; EPICA Community Members, 2006). The paradigm to explain it is that intensifications of the AMOC translate into an increase in northward heat transport at the expense of the southernmost latitudes; conversely, a weakening of the AMOC reduces northward heat transport, thereby warming the south (Crowley, 1992; Stocker, 1998). The different timescale between northern and southern latitudes can be explained by the fact that the Southern Ocean (SO) acts as a heat reservoir that dampens and integrates in time the more rapid North Atlantic signal (Stocker and Johnsen, 2003). The occurrence of H events supports a high sensitivity of Northern Hemisphere (NH) ice sheets as well as their capability to react rapidly (Alvarez-Solas et al., 2013, 2017; Andrews and Voelker, 2018; Hemming, 2004). In the Southern Hemisphere (SH), data showing IRD deposition from the AIS are more scarce. There is evidence of ice discharges from the AIS (Kim et al., 2018; Weber et al., 2012, 2014), but neither a quantification of their contribution in terms of its sea-level equivalent (SLE) nor the identification of their triggering mechanism has yet been done, particularly for events during Marine Isotope Stage 3 (MIS-3). If a periodic deposition of IRD could be found in the SH analogous to the NH, it may hint at an Antarctic response to oceanic changes. This would consolidate the mechanism of the bipolar seesaw and the existence of the heat storage in the SO.
Finally, sea-level reconstructions show fast variations of more than 20 m at millennial timescales during MIS-3 (Frigola et al., 2012; Grant et al., 2012; Rohling et al., 2014) and rises of 4 m per century during meltwater pulse (MWP) 1A at ca. 14.5 ka (Liu et al., 2016) . However, the individual contribution of each paleo ice sheet remains unclear. Due to their location at lower latitudes compared to the AIS, NH ice sheets are more exposed to mass losing processes through atmospheric forcing (ablation). Therefore the majority of those rapid changes are thought to originate in the NH ice sheets (Arz et al., 2007; Ganopolski et al., 2010). However, during MIS-3 sea-level variations fluctuated on the Antarctic rhythm (Grant et al., 2012; Rohling et al., 2009; Siddall et al., 2008), suggesting that a considerable contribution from direct AIS waxing and waning cannot be excluded.
As far as we know, there have been no attempts to simulate Antarctic sea-level contributions at millennial timescales and their potential implications. The aim of this paper is thus to investigate the response of the AIS to millennial-scale variability during the LGP. In particular, we focus on the AIS advance and retreat and its potential sea-level contribution at these timescales. Some assumptions are made for the sake of simplicity, since our aim is to test if the AIS is likely to have responded at millennial timescales and to what extent. For this purpose we use a three-dimensional, thermomechanical, ice sheet–shelf model that is forced through a synthetic climatic forcing including both atmospheric and oceanic changes that evolve temporally through an index deduced from the Dome C deuterium ice-core record. To study the impact of ice–ocean interactions we use a basal melting parameterization that is a function of oceanic temperature anomalies.
The paper is structured as follows: first, the ice-sheet model, the forcing, and the experimental design are described (Sect. 2). Then the response of the AIS to the oceanic forcing is shown, focusing on the ice discharges and grounding line advances at millennial timescales (Sect. 3). Finally, the main results are discussed (Sect. 4) and conclusions summarized (Sect. 5).
2.1 Model
We use the three-dimensional, hybrid, thermomechanical ice-sheet model GRISLI-UCM based on the GRISLI model developed by Ritz et al. (2001) and further extended and tested at the Complutense University of Madrid (see Alvarez-Solas et al., 2017; Tabone et al., 2018). Important changes with respect to the original code include variations in boundary conditions (surface mass balance and basal melt), topography, and new auxiliary modules to calculate the basal drag. Simulations are run on a 40 km×40 km grid with 21 vertical layers corresponding to 157×147 grid points covering the whole Antarctic domain. Initial topographic conditions (ice thickness, surface, and bedrock elevation) are provided from the dataset RTopo-2 (Schaffer et al., 2016), which relies on Bedmap2 (Fretwell et al., 2013) with corrections for ice-shelf cavities. The grounded slow-moving ice, whose flow is dominated by shear processes, is computed by the non-sliding shallow ice approximation (SIA), whereas floating ice shelves, whose evolution is determined by stretching processes, are solved by the shallow shelf approximation (SSA) (Hutter, 1983; MacAyeal, 1989). Intermediate states, in which shearing and stretching regimes can appear simultaneously, are typical of fast-flowing ice streams and are evaluated by summing the velocities of the SIA and SSA. The SSA solution allows for basal sliding and thus includes basal drag depending on the topographic conditions. The model allows basal sliding when the ice base (land–ice interface) is at the melting point and the pressure of the basal water exceeds an imposed threshold.
The total mass balance is given by the difference between accumulation and ablation at the surface, melting at the base of the ice sheet, and ice discharge into the ocean via calving. The surface mass balance (SMB) is determined by atmospheric temperature and precipitation using the positive degree-day scheme (Reeh, 1989). The geothermal heat flux applied as a boundary condition to grounded ice is obtained from the field provided by Shapiro and Ritzwoller (2004). Submarine melt is determined through a linear equation, which transforms oceanic temperature anomalies into melting rates through a heat flux coefficient (details in Sect. 2.2). Calving occurs when the ice-shelf front grid point gets thin enough (200 m) and the incoming ice from upstream does not maintain the necessary ice thickness (Peyaud et al., 2007).
2.2 Forcing method and experimental design
GRISLI-UCM is forced through the same parameterization for atmospheric and oceanic forcing as in Banderas et al. (2018) and Tabone et al. (2018), who used it to specifically investigate the past evolution of the glacial NH and Greenland ice sheets, respectively, but here for the Antarctic domain. In the more general approach used in those studies, oceanic, atmospheric, and precipitation fields are scaled by two climatic indices, an orbital index α(t) (where α=0 represents the LGM state and α=1 the present day, PD), and a millennial index β(t) (β=0 at the LGM, β=1 at the AIM). Because our study focuses on millennial-scale variability, we fix α=0 to maintain constant glacial background conditions. The β index is extracted from the Dome C atmospheric temperature reconstruction (Jouzel and Masson-Delmotte, 2007) and is filtered between 1 and 19 ka to avoid both orbital and submillennial-scale variability. The time evolution of atmospheric temperature (Tatm(t)) and precipitation (P(t)) fields is given by the following equations:
where temperature and precipitation, and PLGM, respectively, are the LGM climatologies calculated from the ERA-Interim reanalysis (Dee et al., 2011) and corrected with orbital anomaly fields obtained from the climatic model of intermediate complexity CLIMBER 3-α (Montoya and Levermann, 2008). The millennial (, δPmil) anomaly fields are obtained from the same climatic model.
The parameterization of the submarine melting rate under floating ice shelves follows a simple linear law based on Beckmann and Goosse (2003):
where Tocn is the oceanic temperature at the corresponding grid point, Tf the freezing point temperature at which the ice base is assumed to be, and κ the heat flux exchange coefficient between ocean and ice. Other possible choices are, for example, a quadratic approach (DeConto and Pollard, 2016; Pattyn, 2017; Pollard and DeConto, 2009). For the sake of simplicity, we assume a linear response between oceanic temperatures and melting rates, which was already tested previously (Alvarez-Solas et al., 2013; Golledge et al., 2015; Philippon et al., 2006; Tabone et al., 2018). The model distinguishes between basal melting at the grounding line (Bgl) and below the ice shelf (Bshlf).
Rignot and Jacobs (2002) have shown that melting rates at the ice shelves are about an order of magnitude lower than those close to the grounding line, and hence we set γ to 0.1. Following the same procedure as for the atmospheric forcing, the oceanic temperature can be rewritten as
where BLGM represents LGM melting rates and the millennial oceanic temperature anomaly. To avoid any accretion at the ice-shelf base, Bgl cannot become lower than 0 m a−1.
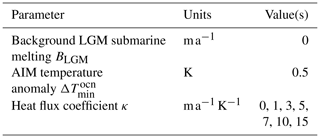
To study the response of the AIS to millennial-scale variability alone, we spun up our model for 120 ka under fixed LGM conditions. Figure 1 illustrates the surface elevation and velocities after the spin-up procedure. We then impose the millennial-scale forcing. The oceanic temperature field and its resulting basal melt rates at the LGM, BLGM, are complicated to obtain due to lack of proxy data. Moreover, BLGM strongly determines the ice extent of the AIS during the LGM. Observations and reconstructions suggest that the ice sheet advanced to the continental shelf break at the LGM (Anderson et al., 2002; Bentley et al., 2014; Denton and Hughes, 2002; Hillenbrand et al., 2012; Kusahara et al., 2015; Whitehouse et al., 2012). Setting BLGM= 0 m a−1 (see Fig. 2a) allows for such an advance. In regions with ocean depths below 2000 m, an artificially large melting rate (50 m a−1) is prescribed to avoid unrealistic ice-shelf growth beyond the continental slope, which would likely be subject to high melt rates in reality because of the intrusion of warm circumpolar deep waters into the ice-shelf cavities (Kusahara et al., 2015). The millennial-scale oceanic temperature anomaly is then obtained from the Dome C ice core (Jouzel and Masson-Delmotte, 2007): the LGM minus present atmospheric temperature at Dome C is estimated to be ca. −10 K and the maximum amplitude of AIM events ca. 2 K. Following Collins et al. (2013) and Golledge et al. (2015), the oceanic amplitude of temperature change is estimated to be up to one-fourth that of the air temperature change, and thus and . Oceanic temperature variations are applied uniformly in space. Figure 3a illustrates the index used for the perturbation. To assess the impact of the ice–ocean interaction we test different oceanic sensitivities. Thus, κ goes from no ice–ocean interaction (0 m a−1 K1) to a large sensitivity (15 m a−1 K1). All values of the tested parameters are provided in Table 1. Finally, sea-level variations are prescribed from Rohling et al. (2014).
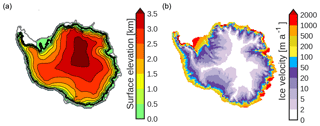
Figure 1Simulated ice-sheet (a) surface elevation (in km) and (b) ice velocities (in m a−1) after the spin-up procedure. The thick black line indicates the simulated grounding line position. The thick grey line represents the continental shelf break (depth 2000 m).
In this section we present our main results focusing on the AIS response to oceanic changes (Fig. 3a) in terms of its SLE contributions (Fig. 3b) and grounding line migrations (Fig. 3c) at millennial timescales. When ignoring the interaction with the ocean (κ=0 m a−1 K1; dark blue curve), no SLE changes are observed, implying that the effect of the atmospheric forcing (temperature and precipitation variations) is negligible. When the oceanic forcing is considered, ice volume subsequently displays millennial-scale variations. The amplitude of these variations increases with increasing oceanic sensitivities (κ values). As long as the climatic index β stays positive, heat is transferred from the ocean to the AIS, ice is discharged from the ice sheet to the ocean, and the grounding line experiences migrations at millennial timescales. When the index becomes negative, the submarine melting is set to zero. In this way oceanic temperatures are assumed to remain close to the freezing point and no accretion is allowed; the ice-sheet volume grows through net accumulation and the ice sheet expands.
Figure 2Mask used to evaluate grounding line migration. (a) Ice extent after glacial spin-up and (b) PD ice extension. Blue zones are model grid cells with grounded ice in marine zones. Grey zones are model grid cells without grounded ice in marine zones but the underlying bathymetry is shallow enough to potentially become grounded (i.e., marine zones with depths less than 2000 m). The thick black line indicates the grounding line position.
To quantify the grounding line migration we introduce a parameter called marine zone occupation (MZO), which is defined as
where NG is the number of model grid cells with grounded ice in marine zones (i.e., zones in which the ice is grounded and its bedrock lies below sea level; see blue zones in Fig. 2a, b) and NP is the number of grid cells of floating ice in marine zones that could potentially become grounded (i.e., zones in which the ice is not grounded but floating and where the underlying bathymetry is shallow enough to potentially become grounded; in practice, we identify these as marine zones with depths above −2000 m; see grey zones in Fig. 2a, b). Therefore, if MZO=1, the grounding line has advanced up to the continental shelf break, grounding all possible marine zones. If MZO is below 0.21, which corresponds to present-day (PD) values (Fig. 2b), the grounding line position has retreated beyond its PD limit. Finally, if MZO=0, the grounding line has entirely retreated up to the land with its bedrock fully above sea level (i.e., marine zones disappear). Figure 3c shows the evolution of the MZO for different oceanic sensitivities. After the spin-up, MZO=0.73 (Fig. 2a). The grounding line has thus advanced towards the continental shelf break but shelves like the Pine Island zone or George Land remain ungrounded (Fig. 1a). For κ=0 the position of the grounding line does not evolve away from the spin-up value. Only when the oceanic forcing is considered do grounding line migrations begin to be appreciable. When oceanic variability is considered, our modeled AIS reacts at millennial timescales.
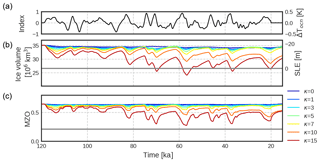
Figure 3(a) Millennial-scale forcing index (β). On the right-hand side the equivalent oceanic temperature anomaly is shown (in K). (b) Ice volume (in 106 km3) and SLE contribution (in m). (c) MZO evolution for different oceanic sensitivities. Colors go from no ice–ocean interaction (, dark blue) to large oceanic sensitivity (, red). The solid grey line in (b) and (c) indicates the present-day value of the ice volume and MZO, respectively.
Figure 4 illustrates the surface elevation (a) and ice velocity (b) for three different oceanic sensitivities (κ=1, 5, and 10 ) after a typical cold phase (at 61 ka). The configuration in the three cases is similar, with an advanced grounding line with grounded Ronne and Ross embayments. The grounding line retreat in the Ross shelf increases with increasing κ. Ice streams also penetrate further inland with increasing κ. Figure 5 illustrates the same fields after an AIM event (at 57 ka). While the lowest sensitivity case (κ=1 m a−1 K1) shows an extensive ice sheet close to the continental shelf break similar to the initial LGM state, as the sensitivity increases (κ=5 m a−1 K1) marine zones such as the Ronne ice shelf begin to retreat and velocities increase. For sufficiently high oceanic sensitivities (κ=10 m a−1 K1) the Ronne and Ross ice shelves experience a substantial retreat during AIM events. In addition, the ice velocity field shows ice streams penetrating further inland with increasing κ. The ice thickness difference between these two snapshots highlights the particular embayments for which the AIS is discharging for increasing ice–ocean sensitivities (see Fig. 6). The majority of the ice loss comes from the Ronne shelf as it is the most vulnerable zone to oceanic warming. The Ross shelf does not experience a substantial ice loss and grounding line retreat until κ>=10 m a−1 K1. The Pine Island zone responds in a similar manner to the oceanic warming but with less impact. Grounding line migrations and ice discharges are not restricted to the WAIS but also occur in the coastal zones of the EAIS, which goes all along the Amery shelf down to Wilkes Land.
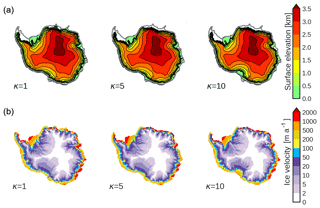
Figure 4Snapshots of the AIS simulations at a cold phase (61 ka) for three different oceanic sensitivities (κ=1, 5, and 10 ). (a) Surface elevation (in km). The thick black line indicates the grounding line position, and the thick grey line is the continental shelf break. (b) Ice velocities (in m a−1).
The longest ice regrowth periods, corresponding to cooling phases, happen between 70 and 60 ka and between 40 and 20 ka. During these periods, for medium to low sensitivities (up to κ=7 m a−1 K1), the grounding line position (as indicated by the MZO) advances close to its LGM value, whereas for high oceanic sensitivities the maximum MZO value reached decreases with increasing κ, indicating the irreversibility typical of hysteresis behavior (Fig. 3c). This suggests that the grounding line can readvance up to the continental shelf break if the oceanic forcing is suppressed long enough, which is not the case for large κ.
We further assess what determines the amplitude of ice discharges between 75 and 15 ka (Fig. 7a). During this time period we find six significant ice discharge events in response to enhanced submarine melting phases, marked with grey shading. Figure 7b shows the ice-volume loss and its corresponding sea-level contribution with respect to κ for every event. Again, for no ice–ocean interaction (κ=0 m a−1 K1) no ice discharges are found, implying that atmospheric millennial variability alone can not produce sea-level variations in the AIS. As the ice–ocean interaction increases with increasing κ, not only does the sea-level contribution of every event increase, but also a wider spread is found between the discharging events, meaning that the sea-level difference between the smallest and largest ice discharge increases. Finally, what determines the total amount of sea-level rise of an AIM event is the total heat exchange between ice and ocean (Fig. 8c). If the amplitude is large, generally major ice discharges will be likely, but if the time interval is too short, then this will not necessarily be true (Fig. 8a). The same is true for the AIM event duration: longer periods will have more potential time to discharge ice, but if the warming is smooth, less melting and ice retreat will happen (Fig. 8b).
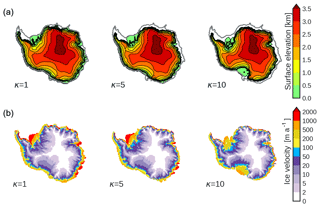
Figure 5Snapshots of the AIS simulations at the end of a warm phase (AIM) event (57 ka) for three different oceanic sensitivities (κ=1, 5, and 10 ). (a) Surface elevation (in km). The thick black line indicates the grounding line position, and the thick grey line is the continental shelf break. (b) Ice velocities (in m a−1).

Figure 6Ice thickness difference between the AIM and the cold phase (AIM minus cold) for different values of oceanic sensitivity (κ=1, 5, and 10 ). Zones with an intense red color illustrate a larger ice difference and hence a major ice loss. The thick blue line illustrates the grounding line position at the cold phase and the thick yellow line the grounding line position at the AIM phase. The thick grey line illustrates the position of the continental shelf break.
Our experimental design follows the bipolar seesaw mechanism (Crowley, 1992; Stocker and Johnsen, 2003) according to which the SO acts as a heat reservoir during millennial-scale AMOC reorganizations. However, the extent to which the SO temperature increases during the slowdown of the AMOC is under debate. Pedro et al. (2018) have argued that the Antarctic Circumpolar Current (ACC) acts as a barrier for heat penetration into the SO and that the postulated heat reservoir is rather provided by the southern subtropical Atlantic and transferred to the AIS by the atmosphere; in addition, oceanic heat transport changes could be compensated for to a large extent by changes in heat transport by the atmosphere and the Pacific Ocean. Changes in SO overturning and/or convection can lead to much larger, albeit localized, warming (e.g., Martin et al., 2013, 2014). Positive feedbacks resulting from sea-ice and ice-shelf melting could further increase warming of the subsurface through enhanced stability of the water column (Weber et al., 2014).
For the sake of simplicity we also considered a spatially homogeneous oceanic warming in phase with the atmospheric temperature reconstruction of Dome C. We deduced the oceanic temperature anomaly from the atmospheric reconstruction of the Dome C ice core. This results in an oceanic temperature anomaly during AIM events of about 0.5 K. To our knowledge, there are no reconstructions available for the SO temperature of high enough temporal resolution. A lower amplitude for the oceanic temperature anomaly in our experimental setup would diminish the effect of the millennial-scale oceanic temperature variability. Nevertheless, our heat transfer coefficient κ can also be interpreted as a weighting parameter of the amount of heat transferred into the SO. However, Buizert et al. (2015) argue that the timing difference between the occurrence of DO events in Greenland ice cores and AIM events provides support for a slow (oceanic) versus a fast (atmospheric) propagation mechanism from north to south. Hence the main question of how much the SO warms up during AIM events is unclear and, again, requires oceanic temperature reconstructions that are yet not available.
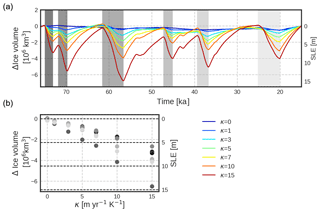
Figure 7(a) Simulated ice volume anomaly between 75 and 15 ka for different values of oceanic sensitivities. Anomalies are calculated relative to the state at 15 ka and detrended between 75 and 15 ka. Grey illustrates significant ice discharging events with increasingly darker grey colors for older events. (b) Scatterplot of the sea-level contribution of every discharging phase with respect to κ.
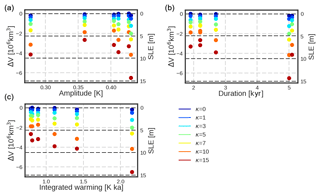
Figure 8Ice-volume discharge and SLE contribution of every event against (a) the amplitude of the warming, (b) the duration of the warming phase, and (c) the integrated warming defined as the peak warming times the duration. Colors represent the different ice–ocean sensitivities.
We also found that if the heat flux transfer parameter between ice and ocean is larger than or equal to 10 m a−1 K1 then the ice sheet is not able to regrow to its initial state after spin-up, neither in volume nor in extent. This highlights the possibility that a heat flux parameter of 10 m a−1 K1 is maybe too large for our ice-sheet model as we know that during the LGM the AIS reached its maximum size from reconstructions.
Here we simulated the grounding line migration at millennial timescales for different oceanic sensitivities. We observed that at those relatively short timescales, the grounding line is capable of advancing to its initial state after retreating. Although here we mainly focus on ice-sheet dynamics, we think this variability could be relevant for brine rejection over the continental shelf as proposed by Paillard and Parrenin (2004). The underlying mechanism is that during grounding line advances, brine (salty water released during sea-ice formation) is pushed out of the continental shelf break. This salty water descends to the bottom of the ocean, having a strong impact on the carbon exchange. If a millennial oscillation of the grounding line took place, it could explain the rise of carbon into the atmosphere, which may be a potential explanation for DO events as well as glacial–interglacial shifts at orbital timescales.
Sea-level reconstructions during MIS-3 show millennial fluctuations that can reach more than 20 m SLE. These sea-level differences are generally attributed to paleo NH ice sheets (Arz et al., 2007). Our results highlight the possibility that a warming of the SO can have a strong impact on the AIS, producing substantial ice discharges. None of our results, including those with a high oceanic sensitivity, exceeded 20 m SLE. Low sensitivities (κ<5 m a−1 K1) do not produce discharging events of more than 5 m, which means that NH paleo ice sheets would still be the major contributors to millennial sea-level fluctuations. For κ>10 m a−1 K1, SLE contributions of more than 10 m occur, which would imply a significant Antarctic contribution as well. However, as discussed above, this contribution (and for larger oceanic sensitivities) seems unrealistic as our model does not support a regrowth of the AIS to the continental shelf break under LGM climate conditions. Intermediate values (κ=7 m a−1 K1) lead to discharges of around 6 m SLE. A non-negligible Antarctic contribution to sea-level changes at millennial timescales during the LGP will have an impact on reconstructing the size of other paleo ice sheets.
We have investigated the response of the AIS to millennial-scale climate variability and, in particular, its response to different oceanic sensitivities using a hybrid, three-dimensional, thermomechanical ice-sheet model. The model is forced using a method that has already been tested (Banderas et al., 2018) and is provided by an improved subglacial melting routine. Because SO temperature reconstructions are not available we assumed that oceanic temperatures covary with atmospheric temperature variations at millennial timescales based on Stocker and Johnsen (2003). Our simulations suggest that, contrary to the idea that the AIS is a slow reactive ice sheet, it could be more reactive to millennial-scale climate variabilities than previously thought. We found that whereas atmospheric millennial-scale variability had no appreciable impact on the AIS, SO warming could produce episodes of ice discharge, leading to substantial sea-level rise and grounding line migration. Although this timescale may seem short for such a large ice sheet, our simulations show, in the range of realistic values for oceanic sensitivities, that considerable grounding line retreat in the Ronne, Ross, and Wilkes Land embayment, as well as sea-level discharge of around 6 m SLE at millennial timescales, can occur. Our results highlight the possibility that, via the bipolar seesaw, a slowdown of the AMOC could have accumulated more heat in the Southern Ocean, resulting in significant sea-level rise produced by the AIS on millennial timescales.
GRISLI-UCM code and the analyzed data are available from the authors upon request.
JB carried out the simulations, analyzed the results, and wrote the paper. All other authors contributed to designing the simulations, analyzing the results, and writing the paper.
The authors declare that they have no conflict of interest.
We are grateful to Catherine Ritz for providing the original model GRISLI and
to Rubén Banderas for helping initially with the model. This work was funded
by the Spanish Ministry of Science and Innovation under the project MOCCA
(Modelling Abrupt Climate Change, grant no. CGL2014-59384-R). Ilaria Tabone
is funded by the Spanish National Programme for the Promotion of Talent and
its Employability (grant no. BES-2015-074097). Alexander Robinson is funded
by the Ramón y Cajal Programme of the Spanish Ministry for Science,
Innovation and Universities. All of these simulations were performed in EOLO,
the HPC of Climate Change of the International Campus of Excellence of
Moncloa, funded by MECD and MICINN.
Edited by: Steven Phipps
Reviewed by: two anonymous referees
Alvarez-Solas, J., Charbit, S., Ramstein, G., Paillard, D., Dumas, C., Ritz, C., and Roche, D. M.: Millennial-scale oscillations in the Southern Ocean in response to atmospheric CO 2 increase, Global Planet. Change, 76, 128–136, https://doi.org/10.1016/j.gloplacha.2010.12.004, 2011. a
Alvarez-Solas, J., Robinson, A., Montoya, M., and Ritz, C.: Iceberg discharges of the last glacial period driven by oceanic circulation changes, P. Natl. Acad. Sci. USA, 110, 16350–16354, https://doi.org/10.1073/pnas.1306622110, 2013. a, b, c
Alvarez-Solas, J., Banderas, R., Robinson, A., and Montoya, M.: Oceanic forcing of the Eurasian Ice Sheet on millennial time scales during the Last Glacial Period, Clim. Past Discuss., https://doi.org/10.5194/cp-2017-143, 2017. a, b
Anderson, J. B., Shipp, S. S., Lowe, A. L., Wellner, J. S., and Mosola, A. B.: The Antarctic Ice Sheet during the Last Glacial Maximum and its subsequent retreat history: a review, Quaternary Sci. Rev., 21, 49–70, https://doi.org/10.1016/S0277-3791(01)00083-X, 2002. a
Andrews, J. T. and Voelker, A. H.: “Heinrich Events” (& sediments): A history of terminology and recommendations for future usage, Quaternary Sci. Rev., 187, 31–40, https://doi.org/10.1016/j.quascirev.2018.03.017, 2018. a
Arz, H. W., Lamy, F., Ganopolski, A., Nowaczyk, N., and Pätzold, J.: Dominant Northern Hemisphere climate control over millennial-scale glacial sea-level variability, Quaternary Sci. Rev., 26, 312–321, https://doi.org/10.1016/j.quascirev.2006.07.016, 2007. a, b
Augustin, L., Barbante, C., Barnes, P. R., Barnola, J. M., Bigler, M., Castellano, E., Cattani, O., Chappellaz, J., Dahl-Jensen, D., Delmonte, B., Dreyfus, G., Durand, G., Falourd, S., Fischer, H., Fluckiger, J., Hansson, M. E., Huybrechts, P., Jugie, G., Johnsen, S. J., Jouzel, J., Kaufmann, P., Kipfstuhl, J., Lambert, F., Lipenkov, V. Y., Littot, G. C., Longinelli, A., Lorrain, R., Maggi, V., Masson-Delmotte, V., Miller, H., Mulvaney, R., Oerlemans, J., Oerter, H., Orombelli, G., Parrenin, F., Peel, D. A., Petit, J.-R., Raynaud, D., Ritz, C., Ruth, U., Schwander, J., Siegenthaler, U., Souchez, R., Stauffer, B., Steffensen, J. P., Stenni, B., Stocker, T. F., Tabacco, I. E., Udisti, R., van der Wal, R. S., van den Broeke, M., Weiss, J., Willhelms, F., Winther, J.-G., Wolff, E. W., and Zucchelli, M.: Eight glacial cycles from an Antarctic ice core, Nature, 429, 623–628, https://doi.org/10.1038/nature02599, 2004. a
Bakker, A. M., Wong, T. E., Ruckert, K. L., and Keller, K.: Sea-level projections representing the deeply uncertain contribution of the West Antarctic ice sheet, Sci. Rep., 7, 3880, https://doi.org/10.1038/s41598-017-04134-5, 2017a. a, b
Bakker, A. M. R., Louchard, D., and Keller, K.: Sources and implications of deep uncertainties surrounding sea-level projections, Climatic Change, 140, 339–347, https://doi.org/10.1007/s10584-016-1864-1, 2017b. a
Bamber, J. L., Riva, R. E., Vermeersen, B. L., and LeBrocq, A. M.: Reassessment of the potential sea-level rise from a collapse of the West Antarctic Ice Sheet, Science, 324, 901–903, https://doi.org/10.1126/science.1169335, 2009. a
Banderas, R., Alvarez-Solas, J., Robinson, A., and Montoya, M.: A new approach for simulating the paleo-evolution of the Northern Hemisphere ice sheets, Geosci. Model Dev., 11, 2299–2314, https://doi.org/10.5194/gmd-11-2299-2018, 2018. a, b
Barker, S., Chen, J., Gong, X., Jonkers, L., Knorr, G., and Thornalley, D.: Icebergs not the trigger for North Atlantic cold events, Nature, 520, 333–336, https://doi.org/10.1038/nature14330, 2015. a
Beckmann, A. and Goosse, H.: A parameterization of ice shelf–ocean interaction for climate models, Ocean Model., 5, 157–170, https://doi.org/10.1016/S1463-5003(02)00019-7, 2003. a
Bentley, M. J., Cofaigh, C. O., Anderson, J. B., Conway, H., Davies, B., Graham, A. G., Hillenbrand, C.-D., Hodgson, D. A., Jamieson, S. S., Larter, R. D., Mackintosh, A., Smith, J. A., Verleyen, E., Ackert, R. P., Bart, P. J., Berg, S., Brunstein, D., Canals, M., Colhoun, E. A., Crosta, X., Dickens, W. A., Domack, E., Dowdeswell, J. A., Dunbar, R., Ehrmann, W., Evans, J., Favier, V., Fink, D., Fogwill, C. J., Glasser, N. F., Gohl, K., Golledge, N. R., Goodwin, I., Gore, D. B., Greenwood, S. L., Hall, B. L., Hall, K., Hedding, D. W., Hein, A. S., Hocking, E. P., Jakobsson, M., Johnson, J. S., Jomelli, V., Jones, R. S., Klages, J. P., Kristoffersen, Y., Kuhn, G., Leventer, A., Licht, K., Lilly, K., Lindow, J., Livingstone, S. J., Massé, G., McGlone, M. S., McKay, R. M., Melles, M., Miura, H., Mulvaney, R., Nela, W., Nitsche, F. O., O'Brien, P. E., Post, A. L., Roberts, S. J., Saunders, K. M., Selkirk, P. M., Simms, A. R., Spiegel, C., Stolldorf, T. D., Sugden, D. E., van der Putten, N., van Ommen, T., Verfaillie, D., Vyverman, W., Wagner, B., White, D. A., Witus, A. E., and Zwartz, D.: A community-based geological reconstruction of Antarctic Ice Sheet deglaciation since the Last Glacial Maximum, Quaternary Sci. Rev., 100, 1–9, https://doi.org/10.1016/j.quascirev.2014.06.025, 2014. a
Blunier, T. and Brook, E. J.: Timing of millennial-scale climate change in Antarctica and Greenland during the last glacial period, Science, 291, 109–112, https://doi.org/10.1126/science.291.5501.109, 2001. a
Böhm, E., Lippold, J., Gutjahr, M., Frank, M., Blaser, P., Antz, B., Fohlmeister, J., Frank, N., Andersen, M., and Deininger, M.: Strong and deep Atlantic meridional overturning circulation during the last glacial cycle, Nature, 517, 73–76, https://doi.org/10.1038/nature14059, 2015. a
Buizert, C., Adrian, B., Ahn, J., Albert, M., Alley, R. B., Baggenstos, D., Bauska, T. K., Bay, R. C., Bencivengo, B. B., Bentley, C. R., Brook, E. J., Chellman, N. J., Clow, G. D., Cole-Dai, J., Conway, H., Cravens, E., Cuffey, K. M., Dunbar, N. W., Edwards, J. S., Fegyveresi, J. M., Ferris, D. G., Fitzpatrick, J. J., Fudge, T. J., Gibson, C. J., Gkinis, V., Goetz, J. J., Gregory, S., Hargreaves, G. M., Iverson, N., Johnson, J. A., Jones, T. R., Kalk, M. L., Kippenhan, M. J., Koffman, B. G., Kreutz, K., Kuhl, T. W., Lebar, D. A., Lee, J. E., Marcott, S. A., Markle, B. R., Maselli, O. J., McConnell, J. R., McGwire, K. C., Mitchell, L. E., Mortensen, N. B., Neff, P. D., Nishiizumi, K., Nunn, R. M., Orsi, A. J., Pasteris, D. R., Pedro, J. B., Pettit, E. C., Price, P. B., Priscu, J. C., Rhodes, R. H., Rosen, J. L., Schauer, A. J., Schoenemann, S. W., Sendelbach, P. J., Severinghaus, J. P., Shturmakov, A. J., Sigl, M., Slawny, K. R., Souney, J. M., Sowers, T. A., Spencer, M. K., Steig, E. J., Taylor, K. C., Twickler, M. S., Vaughn, B. H., Voigt, D. E., Waddington, E. D., Welten, K. C., Wendricks, A. W., White, J. W. C., Winstrup, M., Wong, G. J., and Woodruf, T. E.: Precise interpolar phasing of abrupt climate change during the last ice age, Nature, 520, 661–665, https://doi.org/10.1038/nature14401, 2015. a
Collins, M., Knutti, R., Arblaster, J. M., Dufresne, J. L., Fichefet, T., Friedlingstein, P., Gao, X., Gutowski, W. J., Johns, T., Krinner, G., Shongwe, M., Tebaldi, C., Weaver, A. J., and Wehner, M.: Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, edited by: Stocker, T., Qin, D., Plattner, G., Tignor, M. M. B., Allen, S. K., Boschung, J., Nauels, A., Xia, Y., Bex, V., and Midgley, P. M., Cambridge Univ. Press, 1029–1136, 2013. a
Crowley, T. J.: North Atlantic deep water cools the Southern Hemisphere, Paleoceanography, 7, 489–497, https://doi.org/10.1029/92PA01058, 1992. a, b
Dansgaard, W., Johnsen, S., Clausen, H., Dahl-Jensen, D., Gundestrup, N., Hammer, C., Hvidberg, C., Steffensen, J., Sveinbjörnsdottir, A., Jouzel, J., and Bond, G.: Evidence for general instability of past climate from a 250-kyr ice-core record, Nature, 364, 218–20, https://doi.org/10.1038/364218a0, 1993. a
DeConto, R. M. and Pollard, D.: Contribution of Antarctica to past and future sea-level rise, Nature, 531, 591–597, https://doi.org/10.1038/nature17145, 2016. a, b
Dee, D. P., Uppala, S., Simmons, A., Berrisford, P., Poli, P., Kobayashi, S., Andrae, U., Balmaseda, M., Balsamo, G., Bauer, P., Bechtold, P., Beljaars, A. C. M., van de Berg, L., Bidlot, J., Bormann, N., Delsol, C., Dragani, R., Fuentes, M., Geer, A. J., Haimberger, L., Healy, S. B., Hersbach, H., Holm, E. V., Isaksen, L., Kallberg, P., Kohler, M., Matricardi, M., McNally, A. P., Monge Sanz, B. M., Morcrette, J. J., Park, B. K., Peubey, C., de Rosnay, P., Tavolato, C., Thépaut, J. N., and Vitart, F.: The ERA-Interim reanalysis: Configuration and performance of the data assimilation system, Q. J. Roy. Meteor. Soc., 137, 553–597, https://doi.org/10.1002/qj.828, 2011. a
Denton, G. H. and Hughes, T. J.: Reconstructing the Antarctic ice sheet at the Last Glacial Maximum, Quaternary Sci. Rev., 21, 193–202, https://doi.org/10.1016/S0277-3791(01)00090-7, 2002. a
EPICA Community Members: One-to-one coupling of glacial climate variability in Greenland and Antarctica, Nature, 444, 195–198, https://doi.org/10.1038/nature05301, 2006. a
Favier, L., Durand, G., Cornford, S. L., Gudmundsson, G. H., Gagliardini, O., Gillet-Chaulet, F., Zwinger, T., Payne, A., and Le Brocq, A. M.: Retreat of Pine Island Glacier controlled by marine ice-sheet instability, Nat. Clim. Change, 4, 117–121, https://doi.org/10.1038/nclimate2094, 2014. a
Feldmann, J. and Levermann, A.: Collapse of the West Antarctic Ice Sheet after local destabilization of the Amundsen Basin, P. Natl. Acad. Sci. USA, 112, 14191–14196, https://doi.org/10.1073/pnas.1512482112, 2015. a
Fretwell, P., Pritchard, H. D., Vaughan, D. G., Bamber, J. L., Barrand, N. E., Bell, R., Bianchi, C., Bingham, R. G., Blankenship, D. D., Casassa, G., Catania, G., Callens, D., Conway, H., Cook, A. J., Corr, H. F. J., Damaske, D., Damm, V., Ferraccioli, F., Forsberg, R., Fujita, S., Gim, Y., Gogineni, P., Griggs, J. A., Hindmarsh, R. C. A., Holmlund, P., Holt, J. W., Jacobel, R. W., Jenkins, A., Jokat, W., Jordan, T., King, E. C., Kohler, J., Krabill, W., Riger-Kusk, M., Langley, K. A., Leitchenkov, G., Leuschen, C., Luyendyk, B. P., Matsuoka, K., Mouginot, J., Nitsche, F. O., Nogi, Y., Nost, O. A., Popov, S. V., Rignot, E., Rippin, D. M., Rivera, A., Roberts, J., Ross, N., Siegert, M. J., Smith, A. M., Steinhage, D., Studinger, M., Sun, B., Tinto, B. K., Welch, B. C., Wilson, D., Young, D. A., Xiangbin, C., and Zirizzotti, A.: Bedmap2: improved ice bed, surface and thickness datasets for Antarctica, The Cryosphere, 7, 375–393, https://doi.org/10.5194/tc-7-375-2013, 2013. a, b
Frigola, J., Canals, M., Cacho, I., Moreno, A., Sierro, F. J., Flores, J. A., Berné, S., Jouet, G., Dennielou, B., Herrera, G., Pasqual, C., Grimalt, J. O., Galavazi, M., and Schneider, R.: A 500 kyr record of global sea-level oscillations in the Gulf of Lion, Mediterranean Sea: new insights into MIS 3 sea-level variability, Clim. Past, 8, 1067–1077, https://doi.org/10.5194/cp-8-1067-2012, 2012. a
Fürst, J. J., Durand, G., Gillet-Chaulet, F., Tavard, L., Rankl, M., Braun, M., and Gagliardini, O.: The safety band of Antarctic ice shelves, Nat. Clim. Change, 6, 479–482, https://doi.org/10.1038/nclimate2912, 2016. a
Ganopolski, A. and Rahmstorf, S.: Rapid changes of glacial climate simulated in a coupled climate model, Nature, 409, 153–158, https://doi.org/10.1038/35051500, 2001. a
Ganopolski, A., Calov, R., and Claussen, M.: Simulation of the last glacial cycle with a coupled climate ice-sheet model of intermediate complexity, Clim. Past, 6, 229–244, https://doi.org/10.5194/cp-6-229-2010, 2010. a
Golledge, N. R., Kowalewski, D. E., Naish, T. R., Levy, R. H., Fogwill, C. J., and Gasson, E. G.: The multi-millennial Antarctic commitment to future sea-level rise, Nature, 526, 421–425, https://doi.org/10.1038/nature15706, 2015. a, b, c
Grant, K., Rohling, E., Bar-Matthews, M., Ayalon, A., Medina-Elizalde, M., Ramsey, C. B., Satow, C., and Roberts, A.: Rapid coupling between ice volume and polar temperature over the past 150,000 years, Nature, 491, 744–747, https://doi.org/10.1038/nature11593, 2012. a, b
Hemming, S. R.: Heinrich events: Massive late Pleistocene detritus layers of the North Atlantic and their global climate imprint, Rev. Geophys., 42, RG1005, https://doi.org/10.1029/2003RG000128, 2004. a, b
Henry, L., McManus, J. F., Curry, W. B., Roberts, N. L., Piotrowski, A. M., and Keigwin, L. D.: North Atlantic ocean circulation and abrupt climate change during the last glaciation, Science, 353, 470–474, https://doi.org/10.1126/science.aaf5529, 2016. a
Hillenbrand, C.-D., Melles, M., Kuhn, G., and Larter, R. D.: Marine geological constraints for the grounding-line position of the Antarctic Ice Sheet on the southern Weddell Sea shelf at the Last Glacial Maximum, Quaternary Sci. Rev., 32, 25–47, https://doi.org/10.1016/j.quascirev.2011.11.017, 2012. a
Hutter, K.: Theoretical glaciology; material science of ice and the mechanics of glaciers and ice sheets, D. Reidel Publishing Co./Tokyo, Terra Scintific Publishing Co, 1983. a
Jacobs, S. S., Jenkins, A., Giulivi, C. F., and Dutrieux, P.: Stronger ocean circulation and increased melting under Pine Island Glacier ice shelf, Nat. Geosci., 4, 519–523, https://doi.org/10.1038/ngeo1188, 2011. a
Jouzel, J. and Masson-Delmotte, V.: EPICA Dome C Ice Core 800KYr deuterium data and temperature estimates, 2007. a, b
Kim, S., Yoo, K.-C., Lee, J. I., Lee, M. K., Kim, K., Yoon, H. I., and Moon, H. S.: Relationship between magnetic susceptibility and sediment grain size since the last glacial period in the Southern Ocean off the northern Antarctic Peninsula–Linkages between the cryosphere and atmospheric circulation, Palaeogeogr. Palaeocl., 505, 359–370, https://doi.org/10.1016/j.palaeo.2018.06.016, 2018. a
Kusahara, K., Sato, T., Oka, A., Obase, T., Greve, R., Abe-Ouchi, A., and Hasumi, H.: Modelling the Antarctic marine cryosphere at the Last Glacial Maximum, Ann. Glaciol., 56, 425–435, https://doi.org/10.3189/2015AoG69A792, 2015. a, b
Liu, J., Milne, G. A., Kopp, R. E., Clark, P. U., and Shennan, I.: Sea-level constraints on the amplitude and source distribution of Meltwater Pulse 1A, Nat. Geosci., 9, 130–134, https://doi.org/10.1038/NGEO2616, 2016. a
MacAyeal, D. R.: Large-scale ice flow over a viscous basal sediment: Theory and application to ice stream B, Antarctica, J. Geophys. Res., 94, 4071–4087, https://doi.org/10.1029/JB094iB04p04071, 1989. a
Marcott, S. A., Shakun, J. D., Clark, P. U., and Mix, A. C.: A reconstruction of regional and global temperature for the past 11,300 years, Science, 339, 1198–1201, https://doi.org/10.1126/science.1228026, 2013. a
Martin, T., Park, W., and Latif, M.: Multi-centennial variability controlled by Southern Ocean convection in the Kiel Climate Model, Clim. Dynam., 40, 2005–2022, https://doi.org/10.1007/s00382-012-1586-7, 2013. a
Martin, T., Steele, M., and Zhang, J.: Seasonality and long-term trend of Arctic Ocean surface stress in a model, J. Geophys. Res.-Oceans, 119, 1723–1738, https://doi.org/10.1002/2013JC009425, 2014. a
Martín-Español, A., Zammit-Mangion, A., Clarke, P. J., Flament, T., Helm, V., King, M. A., Luthcke, S. B., Petrie, E., Rémy, F., Schön, N., Wouters, B., and Bamber, J. L.: Spatial and temporal Antarctic Ice Sheet mass trends, glacio-isostatic adjustment, and surface processes from a joint inversion of satellite altimeter, gravity, and GPS data, J. Geophys. Res.-Earth, 121, 182–200, https://doi.org/10.1002/2015JF003550, 2016. a
McManus, J. F., Francois, R., Gherardi, J.-M., Keigwin, L. D., and Brown-Leger, S.: Collapse and rapid resumption of Atlantic meridional circulation linked to deglacial climate changes, Nature, 428, 834–837, https://doi.org/10.1038/nature02494, 2004. a
Mercer, J. H.: West Antarctic ice sheet and CO2 greenhouse effect- A threat of disaster, Nature, 271, 321–325, https://doi.org/10.1038/271321a0, 1978. a
Montoya, M. and Levermann, A.: Surface wind-stress threshold for glacial Atlantic overturning, Geophys. Res. Lett., 35, L03608, https://doi.org/10.1029/2007GL032560, 2008. a
Nicholls, R. J. and Cazenave, A.: Sea-level rise and its impact on coastal zones, Science, 328, 1517–1520, https://doi.org/10.1126/science.1185782, 2010. a
Paillard, D. and Parrenin, F.: The Antarctic ice sheet and the triggering of deglaciations, Earth Planet. Sc. Lett., 227, 263–271, https://doi.org/10.1016/j.epsl.2004.08.023, 2004. a
Paolo, F. S., Fricker, H. A., and Padman, L.: Volume loss from Antarctic ice shelves is accelerating, Science, 348, 327–331, https://doi.org/10.1126/science.aaa0940, 2015. a
Pattyn, F.: Sea-level response to melting of Antarctic ice shelves on multi-centennial timescales with the fast Elementary Thermomechanical Ice Sheet model (f.ETISh v1.0), The Cryosphere, 11, 1851–1878, https://doi.org/10.5194/tc-11-1851-2017, 2017. a
Pedro, J. B., Jochum, M., Buizert, C., He, F., Barker, S., and Rasmussen, S. O.: Beyond the bipolar seesaw: Toward a process understanding of interhemispheric coupling, Quaternary Sci. Rev., 192, 27–46, https://doi.org/10.1016/j.quascirev.2018.05.005, 2018. a
Petit, J.-R., Jouzel, J., Raynaud, D., Barkov, N. I., Barnola, J.-M., Basile, I., Bender, M., Chappellaz, J., Davis, M., Delaygue, G., Delmotte, M., Kotlyakov, V. M., Legrand, M., Lipenkov, V. Y., Lorius, C., Pépin, L., Ritz, C., Saltzman, E., and Stievenard, M.: Climate and atmospheric history of the past 420,000 years from the Vostok ice core, Antarctica, Nature, 399, 429–436, https://doi.org/10.1038/20859, 1999. a
Peyaud, V., Ritz, C., and Krinner, G.: Modelling the Early Weichselian Eurasian Ice Sheets: role of ice shelves and influence of ice-dammed lakes, Clim. Past, 3, 375–386, https://doi.org/10.5194/cp-3-375-2007, 2007. a
Philippon, G., Ramstein, G., Charbit, S., Kageyama, M., Ritz, C., and Dumas, C.: Evolution of the Antarctic ice sheet throughout the last deglaciation: a study with a new coupled climate-north and south hemisphere ice sheet model, Earth Planet. Sc. Lett., 248, 750–758, https://doi.org/10.1016/j.epsl.2006.06.017, 2006. a
Pollard, D. and DeConto, R. M.: Modelling West Antarctic ice sheet growth and collapse through the past five million years, Nature, 458, 329–332, https://doi.org/10.1038/nature07809, 2009. a
Rahmstorf, S.: Ocean circulation and climate during the past 120,000 years, Nature, 419, 207–214, https://doi.org/10.1038/nature01090, 2002. a
Reeh, N.: Parameterization of melt rate and surface temperature on the Greenland ice sheet, J. Geophys. Res.-Sol. Ea., 59, 113–128, 1989. a
Rignot, E. and Jacobs, S. S.: Rapid bottom melting widespread near Antarctic ice sheet grounding lines, Science, 296, 2020–2023, https://doi.org/10.1126/science.1070942, 2002. a
Rignot, E., Casassa, G., Gogineni, P., Krabill, W., Rivera, A. U., and Thomas, R.: Accelerated ice discharge from the Antarctic Peninsula following the collapse of Larsen B ice shelf, Geophys. Res. Lett., 31, L18401, https://doi.org/10.1029/2004GL020697, 2004. a
Rignot, E., Jacobs, S., Mouginot, J., and Scheuchl, B.: Ice-shelf melting around Antarctica, Science, 341, 266–270, https://doi.org/10.1126/science.1235798, 2013. a
Ritz, C., Rommelaere, V., and Dumas, C.: Modeling the evolution of Antarctic ice sheet over the last 420,000 years: Implications for altitude changes in the Vostok region, J. Geophys. Res.-Atmos., 106, 31943–31964, https://doi.org/10.1029/2001JD900232, 2001. a
Rohling, E., Foster, G. L., Grant, K., Marino, G., Roberts, A., Tamisiea, M. E., and Williams, F.: Sea-level and deep-sea-temperature variability over the past 5.3 million years, Nature, 508, 477–482, https://doi.org/10.1038/nature13230, 2014. a, b
Rohling, E. J., Grant, K., Bolshaw, M., Roberts, A., Siddall, M., Hemleben, C., and Kucera, M.: Antarctic temperature and global sea level closely coupled over the past five glacial cycles, Nat. Geosci., 2, 500–504, https://doi.org/10.1038/ngeo557, 2009. a
Ruth, U., Barnola, J.-M., Beer, J., Bigler, M., Blunier, T., Castellano, E., Fischer, H., Fundel, F., Huybrechts, P., Kaufmann, P., Kipfstuhl, S., Lambrecht, A., Morganti, A., Oerter, H., Parrenin, F., Rybak, O., Severi, M., Udisti, R., Wilhelms, F., and Wolff, E.: “EDML1”: a chronology for the EPICA deep ice core from Dronning Maud Land, Antarctica, over the last 150 000 years, Clim. Past, 3, 475–484, https://doi.org/10.5194/cp-3-475-2007, 2007. a
Schaffer, J., Timmermann, R., Arndt, J. E., Kristensen, S. S., Mayer, C., Morlighem, M., and Steinhage, D.: A global, high-resolution data set of ice sheet topography, cavity geometry, and ocean bathymetry, Earth Syst. Sci. Data, 8, 543–557, https://doi.org/10.5194/essd-8-543-2016, 2016. a
Schoof, C.: Ice sheet grounding line dynamics: Steady states, stability, and hysteresis, J. Geophys. Res.-Earth, 112, F03S28, https://doi.org/10.1029/2006JF000664, 2007. a
Shaffer, G., Olsen, S. M., and Bjerrum, C. J.: Ocean subsurface warming as a mechanism for coupling Dansgaard-Oeschger climate cycles and ice-rafting events, Geophys. Res. Lett., 31, L24202, https://doi.org/10.1029/2004GL020968, 2004. a
Shapiro, N. M. and Ritzwoller, M. H.: Inferring surface heat flux distributions guided by a global seismic model: particular application to Antarctica, Earth Planet. Sc. Lett., 223, 213–224, https://doi.org/10.1016/j.epsl.2004.04.011, 2004. a
Shepherd, A., Ivins, E., Rignot, E., Smith, B., van den Broeke, M., Velicogna, I., Whitehouse, P., Briggs, K., Joughin, I., Krinner, G., Nowicki, S., Payne, T., Scambos, T., Schlegel, N., A, G., Agosta, C., Ahlstrøm, A., Babonis, G., Barletta, V., Blazquez, A., Bonin, J., Csatho, B., Cullather, R., Felikson, D., Fettweis, X., Forsberg, R., Gallee, H., Gardner, A., Gilbert, L., Groh, A., Gunter, B., Hanna, E., Harig, C., Helm, V., Horvath, A., Horwath, M., Khan, S., Kjeldsen, K. K., Konrad, H., Langen, P., Lecavalier, B., Loomis, B., Luthcke, S., McMillan, M., Melini, D., Mernild, S., Mohajerani, Y., Moore, P., Mouginot, J., Moyano, G., Muir, A., Nagler, T., Nield, G., Nilsson, J., Noel, B., Otosaka, I., Pattle, M. E., Peltier, W. R., Pie, N., Rietbroek, R., Rott, H., Sandberg-Sørensen, L., Sasgen, I., Save, H., Scheuchl, B., Schrama, E., Schröder, L., Seo, K.-W., Simonsen, S., Slater, T., Spada, G., Sutterley, T., Talpe, M., Tarasov, L., van de Berg, W. J., van der Wal, W., van Wessem, M., Vishwakarma, B. D., Wiese, D., and Wouters, B.: Mass balance of the Antarctic Ice Sheet from 1992 to 2017, Nature, 556, 219–222, https://doi.org/10.1038/s41586-018-0179-y, 2018. a
Siddall, M., Rohling, E. J., Thompson, W. G., and Waelbroeck, C.: Marine isotope stage 3 sea level fluctuations: data synthesis and new outlook, Rev. Geophys., 46, RG4003, https://doi.org/10.1029/2007RG000226, 2008. a
Stocker, T. F.: The seesaw effect, Science, 282, 61–62, https://doi.org/10.1126/science.282.5386.61, 1998. a
Stocker, T. F. and Johnsen, S. J.: A minimum thermodynamic model for the bipolar seesaw, Paleoceanography, 18, 1087, https://doi.org/10.1029/2003PA000920, 2003. a, b, c
Sutter, J., Gierz, P., Grosfeld, K., Thoma, M., and Lohmann, G.: Ocean temperature thresholds for Last Interglacial West Antarctic Ice Sheet collapse, Geophys. Res. Lett., 43, 2675–2682, https://doi.org/10.1002/2016GL067818, 2016. a
Tabone, I., Blasco, J., Robinson, A., Alvarez-Solas, J., and Montoya, M.: The sensitivity of the Greenland Ice Sheet to glacial-interglacial oceanic forcing, Clim. Past, 14, 455–472, https://doi.org/10.5194/cp-14-455-2018, 2018. a, b, c
Weber, M., Kuhn, G., Sprenk, D., Rolf, C., Ohlwein, C., and Ricken, W.: Dust transport from Patagonia to Antarctica–a new stratigraphic approach from the Scotia Sea and its implications for the last glacial cycle, Quaternary Sci. Rev., 36, 177–188, https://doi.org/10.1016/j.quascirev.2012.01.016, 2012. a
Weber, M., Clark, P., Kuhn, G., Timmermann, A., Sprenk, D., Gladstone, R., Zhang, X., Lohmann, G., Menviel, L., Chikamoto, M., Friedrich, T., and Ohlwein, C.: Millennial-scale variability in Antarctic ice-sheet discharge during the last deglaciation, Nature, 510, 134–138, https://doi.org/10.1038/nature13397, 2014. a, b
Weertman, J.: Stability of the junction of an ice sheet and an ice shelf, J. Glaciol., 13, 3–11, https://doi.org/10.3189/S0022143000023327, 1974. a
Whitehouse, P. L., Bentley, M. J., and Le Brocq, A. M.: A deglacial model for Antarctica: geological constraints and glaciological modelling as a basis for a new model of Antarctic glacial isostatic adjustment, Quaternary Sci. Rev., 32, 1–24, https://doi.org/10.1016/j.quascirev.2011.11.016, 2012. a