the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Insensitivity of alkenone carbon isotopes to atmospheric CO2 at low to moderate CO2 levels
Marcus P. S. Badger
Thomas B. Chalk
Gavin L. Foster
Paul R. Bown
Samantha J. Gibbs
Philip F. Sexton
Daniela N. Schmidt
Heiko Pälike
Andreas Mackensen
Richard D. Pancost
Atmospheric pCO2 is a critical component of the global carbon system and is considered to be the major control of Earth's past, present, and future climate. Accurate and precise reconstructions of its concentration through geological time are therefore crucial to our understanding of the Earth system. Ice core records document pCO2 for the past 800 kyr, but at no point during this interval were CO2 levels higher than today. Interpretation of older pCO2 has been hampered by discrepancies during some time intervals between two of the main ocean-based proxy methods used to reconstruct pCO2: the carbon isotope fractionation that occurs during photosynthesis as recorded by haptophyte biomarkers (alkenones) and the boron isotope composition (δ11B) of foraminifer shells. Here, we present alkenone and δ11B-based pCO2 reconstructions generated from the same samples from the Pliocene and across a Pleistocene glacial–interglacial cycle at Ocean Drilling Program (ODP) Site 999. We find a muted response to pCO2 in the alkenone record compared to contemporaneous ice core and δ11B records, suggesting caution in the interpretation of alkenone-based records at low pCO2 levels. This is possibly caused by the physiology of CO2 uptake in the haptophytes. Our new understanding resolves some of the inconsistencies between the proxies and highlights that caution may be required when interpreting alkenone-based reconstructions of pCO2.
- Article
(6779 KB) -
Supplement
(118 KB) - BibTeX
- EndNote
Understanding the absolute level and evolution of atmospheric pCO2 through geological time is essential to our understanding of the Earth's climate system. As both a fundamental first-order control and a contributor to multiple dynamic feedbacks, atmospheric pCO2 is critical in setting Earth's surface temperature (Lacis et al., 2010). Reconstructing pCO2 evolution improves the understanding of both the mechanisms behind past climate change (Chalk et al., 2017) and provides novel constraints on climate sensitivities (PALAEOSENS, 2012; Martínez-Botí et al., 2015). This then allows ground truthing of our understanding the climate and the Earth system models that are used for predicting future climate change.
Over the past two decades, two common marine-based CO2 proxies have emerged – alkenone-based εp values (), utilizing the carbon isotopic fractionation imparted during photosynthesis in a subgroup of haptophytes (Bidigare et al., 1997), and planktic foraminiferal δ11B values (), based on the pH control of boron speciation and isotopic fractionation in seawater (Hemming and Hanson, 1992). Multiple records of atmospheric pCO2 now exist for the Cenozoic from both methods, showing a broadly similar long-term trend from a high-CO2 greenhouse world of the early Cenozoic, when CO2 exceeded 400 µatm and may have been higher than 1000 µatm, to a low-CO2 bipolar glaciated world of the Late Pleistocene, when CO2 fell to below 300 µatm (Pagani et al., 2005, 2011; Pearson et al., 2009; Anagnostou et al., 2016; Foster et al., 2017; Sosdian et al., 2018; Super et al., 2018).
However, discrepancies have recently become apparent between both methods when applied to the last 20 Ma (Badger et al., 2013a, b). Specifically, the reconstructions often suggest a lower magnitude of short-term pCO2 change compared to that from (Badger et al., 2013b). Whilst this could be partially explained by mismatches between the sampling intervals, or by the influence of local surface water disequilibrium with the atmosphere with respect to CO2, this discrepancy remains even for records generated from exactly the same sediment samples (Badger et al., 2013b vs. Martínez-Botí et al., 2015). Both the and have been used to estimate Earth system sensitivity in the Pliocene with differing results, with suggesting a higher-than-present Earth system sensitivity Pliocene (7–10 ∘C per CO2 doubling; Pagani et al., 2009), whilst records sensitivity in line with our estimates for today (< 5 ∘C per CO2 doubling; Martínez-Botí et al., 2015). Although this is at least partly due to the different approaches used to calculate Earth system sensitivity in the two studies, it is also due to the differences in reconstructed pCO2 from the two approaches.
The and palaeobarometers are both based on mechanistic frameworks that have been calibrated in either the modern ocean or laboratory culture (Bidigare et al., 1997; Hemming and Hanson, 1992; Sanyal and Hemming, 1996; Pagani et al., 2002). These proxies can be further ground truthed in the recent geological past, when ice core records provide high-quality pCO2 data for the last 800 kyr (Bereiter et al., 2015 and Table 1). In previous work, both (Sanyal et al., 1995; Hönisch and Hemming, 2005; Foster, 2008; Henehan et al., 2013; Foster and Sexton, 2014; Chalk et al., 2017) and (Jasper and Hayes, 1990) have yielded pCO2 records similar in absolute value and amplitude of change to those derived from ice cores. However, the emerging discrepancies between the two methods (Badger et al., 2013a, b; Martínez-Botí et al., 2015) necessitate revisiting this validation, both between the two proxies and between marine proxy and ice core reconstructions.
The ice cores record the pCO2 of the Pleistocene glacial–interglacial cycles (Bereiter et al., 2015 and Table 1) and provide an opportunity for cross-calibrating proxy methods for determining atmospheric pCO2 in the geological archive ( and ) with the direct-CO2 measurements from the ice cores.
Study site
Ocean Drilling Program (ODP) Site 999 is located in the Caribbean Sea (12∘44.639′ N, 78∘44.360′ W; 2838 m water depth; Fig. 1), has an orbitally calibrated age model, and has been used previously for CO2 reconstructions. Our temporal sampling resolution is ∼6 kyr in the Pleistocene and ∼9 kyr in the Pliocene. Although and are independent of one another in many respects, they both rely on assumptions about the equilibrium of surface seawater with the atmosphere with respect to CO2, sea surface temperature, and on well-constrained age models, which can make direct comparison between records from different sites difficult. Here, we overcome these problems by producing and records from identical horizons in the same deep-ocean sediment core in (1) the late Pleistocene, permitting direct comparison to ice core data (Figs. 2a, 3), and (2) across the intensification of Northern Hemisphere glaciation (INHG) in the Pliocene (Seki et al., 2010; Martínez-Botí et al., 2015) (Fig. 2b).
In terms of CO2, ODP Site 999 in the Caribbean Sea is today slightly out of equilibrium with the atmosphere, with surface waters a little oversaturated in CO2, providing a small net source of CO2 to the atmosphere (∼21 µatm; Takahashi et al., 2009). However, the site has been shown to be suitable for recording past changes in pCO2 (Foster, 2008; Foster and Sexton, 2014) and the air–sea equilibrium is not thought to have changed significantly from the Pliocene to today (see discussion in Bartoli et al., 2011). It is one of few sites where both alkenone and boron isotope records can be acquired given the good preservation of both foraminifera and organic matter (Foster, 2008; Badger et al., 2013b; Foster and Sexton, 2014; Martínez-Botí et al., 2015), and Pliocene records of both are available (Bartoli et al., 2011; Badger et al., 2013b; Martínez-Botí et al., 2015). It also has been demonstrated previously to record glacial–interglacial cycles of pH ∕ CO2 (Foster, 2008; Henehan et al., 2013) and a Pleistocene record from 0 to 250 ka has been recently published (Chalk et al., 2017).
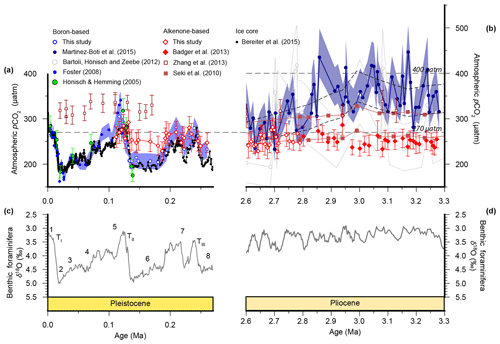
Figure 2Atmospheric CO2 reconstructions through the Plio-Pleistocene. (a) Published boron isotope records from ODP Site 999: open blue circles (Chalk et al., 2017), filled bright blue circles (Foster, 2008; recalculated as described in the text), open grey circles (Bartoli et al., 2011), and filled dark blue circles (Martínez-Botí et al., 2015); and Deep Sea Drilling Project (DSDP) Site 668: filled green circles (Hönisch and Hemming, 2005). (b) Published records from ODP Site 925: open maroon squares (Zhang et al., 2013); ODP Site 999: filled red diamonds (Badger et al., 2013a); and ice core records: filled black squares (Bereiter et al., 2015 and Table 1), as well as our new alkenone isotope records from ODP Site 999 (open red diamonds). The lith size-corrected (dashed black envelope) and uncorrected (solid red envelope) data of Seki et al. (2010) are also shown. All records are shown with 1σ uncertainties as described elsewhere. (c) The benthic foraminiferal stable oxygen isotope stack (Lisiecki and Raymo, 2005) with Marine Isotope Stage (MIS; numerals) and terminations (T) indicated.
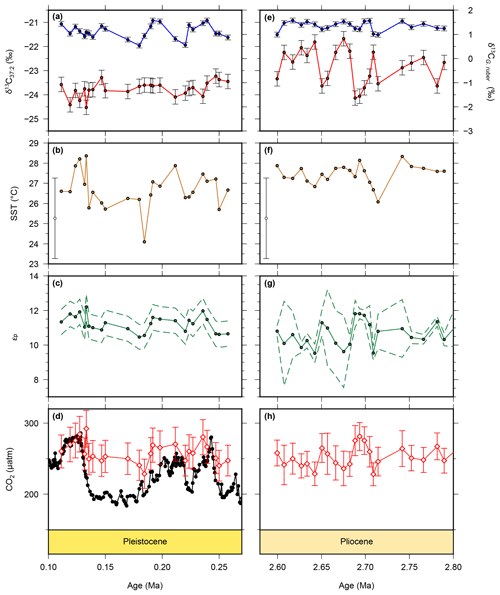
Figure 3New and recalculated data for for the Pleistocene and Pliocene from ODP Site 999. Alkenone δ13C values are shown as red circles for the Pleistocene (a) and Pliocene (b), with G. ruber δ13C from the same samples shown in blue. Alkenone unsaturation-derived SST is shown for the Pleistocene (b) and Pliocene (f). The Pliocene SST data have been previously published in Davis et al. (2013) and are from the same samples as our alkenone δ13C values. Calculated εp data are for the Pleistocene (c) and Pliocene (g) and atmospheric pCO2 from for the Pleistocene (d) and Pliocene (h) (red diamonds). Ice core pCO2 data are shown for the Pleistocene (black circles) for comparison (Bereiter et al., 2015 and Table 1).
2.1 Alkenone isotopes
Our new alkenone-based CO2 record was calculated following Badger et al. (2013b), with modern-day phosphate used in the estimation of the “b” term, ' temperatures, and modern-day salinity (35 psu). Samples were freeze dried, ground to a fine powder by hand, and extracted by Soxhlet apparatus using a dichloromethane (DCM) ∕ methanol azeotrope (2:1, v∕v) refluxing for 24 h. Total lipid extracts were divided into three fractions (F) by small (4 cm) silica chromatography columns, with fractions eluting in 3 mL of n-hexane (F1), DCM (F2), and ethyl acetate ∕n-hexane (1:3, v:v, F3), respectively. Alkenones are eluted in F2. Alkenone identification was confirmed by gas chromatography (GC) mass spectrometry (ThermoQuest Trace MS, He carrier gas). Alkenone isotope analyses were performed using a Thermo Fisher Delta V connected via a GC isolink and ConFlo IV to a Trace GC. The GC oven was programmed to increase in temperature from 70 to 200 ∘C at 20 ∘C min−1, then to 300 ∘C at 6 ∘C min−1 and held isothermal for 25 min. Conversion to Vienna Pee Dee Belemnite (VPDB) was performed by reference to a laboratory standard gas of known δ13C and system performance was monitored using in-house fatty acid methyl ester and n-alkane standard mixtures of known isotopic composition. Long-term precision is approximately 0.3 ‰. To estimate sea surface temperature (SST), the F2 fraction was also analysed by GC-flame ionization detection (Hewlett Packard 5890 Series II), and the GC oven was programmed to increase in temperature from 70 to 130 ∘C at 20 ∘C min−1, then to 300 ∘C at 4 ∘C min−1 and held isothermal for 25 min. An approximately 50 m, 0.32 mm internal diameter capillary column with a 0.12 µm thick dimethylpolysiloxane equivalent film. A H2 carrier gas was used, and quantification was monitored using a hexadecan-2-ol standard added prior to column chromatography. System performance as monitored with an in-house fatty acid methyl ester standard. Alkenone ratios were converted to SST using the global core-top calibration of Müller et al. (1998). Although this is a linear calibration, our uncertainty treatment (see below) should encompass any minor deviation from linear as approaches 1 (see also the discussion in Badger et al., 2013b). All alkenone analyses were carried out at the Bristol node of the NERC Life Sciences Mass Spectrometry Facility hosted by the Organic Geochemistry Unit, University of Bristol.
The alkenone isotope δ13C value is used to calculate the total carbon isotope fractionation that occurs during algal growth (εp). This isotopic fractionation has been shown to be controlled by [CO2(aq)] (Eq. 1; Jasper and Hayes, 1990) which can then be converted to atmospheric CO2 using Henry's law.
To calculate εp from alkenone δ13C values, the carbon isotopic composition of dissolved inorganic carbon (DIC) is required; this is calculated from planktic foraminiferal calcite δ13C, whilst the fractionation which occurs during carbon fixation (εf) is assumed constant here. The b term is the sum of other physiological factors (such as growth rate, cell size, and light limitation) which is estimated from the relationship shown in the modern ocean between b and dissolved reactive phosphate . Further details of the treatment are detailed in Badger et al. (2013b).
Error bars in relevant figures are all 1 SD and based on a full Monte Carlo propagation (n= 10 000) of the following uncertainties: ±2 ∘C and ±0.1 ‰ were applied to temperature and foraminiferal calcite δ13C (normal probability function (pdf); 2σ error) and ±2 and ±0.1 to salinity and , respectively (2σ; uniform pdf). Uncertainties on alkenone δ13C were estimated from replicate runs and calcite δ13C from repeat runs of an internal standard. Integrated analytical and calibration uncertainties for alkenone-based temperatures were estimated and conservative estimates of likely variation for salinity and were used. An 11 % error on the slope of b=a +c was assumed, where a=116.96 and c=81.41 (Pagani et al., 1999).
For consistency with the record for this site, we now adjust for the disequilibrium by subtracting the present-day CO2 surplus and thus recalculate the included values of Badger et al. (2013b) accordingly. SSTs for our new Pliocene data were published in Davis et al. (2013).
2.2 Boron isotopes
Boron isotope data were published in Chalk et al. (2017) and are from the same core samples as our alkenone measurements. Globigerinoides ruber sensu stricto (white, n∼200 individuals from 300 to 355 µm) samples were measured for boron isotope composition on Thermo Scientific Neptune multicollector inductively coupled plasma mass spectrometer (MC-ICP-MS) at the University of Southampton according to methods described elsewhere (Rae et al., 2011; Foster et al., 2013; Martínez-Botí et al., 2015). Analytical uncertainty is given by the external reproducibility of repeat analyses of Japanese Geological Survey Porites coral standard (JCP) at the University of Southampton following Henehan et al. (2013) and is typically < 0.2 ‰ (at 95 % confidence). Metal element to calcium ratios (Li, Mg, B, Na, Al, Mn, Ba, Sr, Cd, U, Nd, and Fe) were analysed using an Thermo Element 2XR ICP-MS at the University of Southampton). Here, these data are used to assess adequacy of clay removal (Al ∕ Ca < 100 µmol mol−1) and to generate down core temperature. pH and CO2 were calculated using a Monte Carlo approach (uncertainties are 2 SD, n= 10 000 replicates) using R (R Core Team, 2015). For pH, we use a boron isotopic composition of seawater of 39.6 ‰ (2 SD of 0.1; Foster et al., 2010) and experimentally determined isotopic fractionation factor (1.027; Klochko et al., 2006), as well as the species-specific calibration for G. ruber of Henehan et al. (2013) (also with incorporated uncertainties). For the CO2 calculations, we use a range of salinity (equal to that used in the calculations) and total alkalinity (TA) that encompasses the modern values (34–37 and 2100–2500 µM, respectively, both with a uniform rather than normal probability distribution. Temperature was determined using Mg ∕ Ca of G. ruber following established methods; Delaney and Boyle, 1985; Evans and Müller, 2012). Mg ∕ Ca SST of planktic foraminifera is used for and alkenone for so that the carrier organisms for the CO2 reconstruction and SST measurements match, ensuring the temperature measurement is coming from the appropriate part of the water column. Inorganic chemical constants were used from the seacarb package in R (Gattuso et al., 2015) and using published values for the p (dissociation constant for boric acid) (Dickson, 1990). Reconstructed atmospheric CO2 values from Foster (2008) were recalculated to match this approach. All uncertainties are included in our simulation and are roughly equivalent to those assumed for the alkenone data and are exactly the same as those used for Martinez-Boti et al. (2015), excluding the δ11Bsw, thus providing a fair comparison.
2.3 Coccolith length measurements
The uptake of CO2 into the coccolithophore cell is affected by the cell size and geometry; using alkenones limits the variation of cell geometry by restricting the source organism to one with exclusively spherical cells (Laws et al., 1997; Popp et al., 1998), but some change in cell size is possible. Coccolith size is used as an semi-quantitative proxy for cell size because coccolith size is typically larger on larger cells, with that relationship being broadly consistent within a single taxonomic group where growth behaviour is broadly comparable (Henderiks, 2008; Gibbs et al., 2013; Sheward et al., 2017). Long-axis coccolith length measurements were therefore taken from 100 specimens of the family Noelaerhabdaceae per sample from standard smear slides. Specimens were imaged at 1500× magnification and measured using CellD software.
To investigate the potential influence of changing cell size on , Eq. (1) can be adapted:
with b′ calculated from using the volume to surface area ratio (V : SA) of modern and fossil coccospheres (Eq. 3; Henderiks and Pagani, 2007):
V : SAEhux is 0.9±0.1 µm in modern haptophytes (Popp et al., 1998) and V : SAfossil can be estimated from lith size measurements (Eq. 4; Henderiks and Pagani, 2007):
2.4 Age model
For the 0–500 ka interval, we generated a detailed age model by tuning the planktic foraminifer (G. ruber) δ18O record from Site 999 (at ∼0.5 to 2.0 kyr resolution) (Schmidt et al., 2006) to the LR04 benthic δ18O stack (Lisiecki and Raymo, 2005) using the AnalySeries software (Paillard et al., 1996). The Pliocene portion of Site 999 is part the LR04 stack and that astronomically tuned age model is used here (Lisiecki and Raymo, 2005).
2.5 Bayesian exploration of input variables
In order to examine the influence of the various input parameters for the calculation of pCO2 from alkenone δ13C values, we carry out a second set of Monte Carlo simulations (n= 100 000) with expanded uncertainty. In this case, we more fully explore uncertainty space using the following input uncertainties (at 95 % confidence or full range): SST (normal distribution, ±6 ∘C), εf (uniform distribution, 24 to 28), b (normal distribution, ±40), and CO2 disequilibrium (20±20). These input distributions are our prior distributions. We then evaluate the CO2 output for each alkenone sample against synchronous ice core pCO2 and boron isotope pCO2 for the Pleistocene and Pliocene, respectively. By only selecting those simulated alkenone pCO2 levels that agree with ice core or p (including associated uncertainties), we can reevaluate the input distributions (our posterior) and gain insights into the relative importance of each of the input variables in potentially driving the observed disagreement in pCO2. Uncertainties in the p are as described above, and we apply an uncertainty of ±6 ppm (2 s) for the ice core pCO2 record (Ahn et al., 2012).
Alkenone and G. ruber δ13C values (Fig. 3a, e) were used to calculate εp values (Fig. 3c, g). Alkenone δ13C values are relatively stable through the Pleistocene portion of the record, varying between −24.5 ‰ and −23.2 ‰. Values are slightly higher in the Pliocene, varying between −24.1 ‰ and −21.7 ‰. G. ruber δ13C values are relatively stable through the whole record, varying between 0.53 ‰ and 1.57 ‰. These give rise to εp values which are similarly fairly stable, varying between 10.5 ‰ and 12.2 ‰ in the Pleistocene, and between 9.53 ‰ and 11.8 ‰ in the Pliocene. Our SST (Fig. 3c, g) record shows warmer temperatures in the Pliocene of around 27 ∘C, with cooler temperatures recorded in the Pleistocene, with the coldest SST recorded in the glacial which is ∼2 ∘C cooler than the interglacial. These records are combined (see methods section) to produce the pCO2 record (Figs. 2, 3c, f), which shows largely stable and invariant values through both the Pliocene and Pleistocene portions of our record.
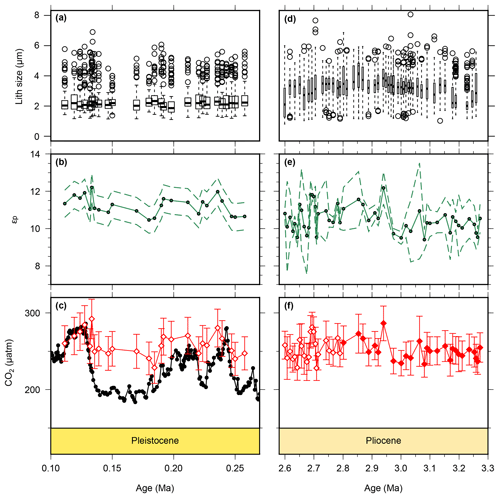
Figure 4Lith size data for samples used for CO2 calculations. Pleistocene lith size (a) are from this study, whilst Pliocene (b) values were published previously (Davis et al., 2013) but are from the same samples as our CO2 estimates. Pleistocene εp (b) are from this study, whilst the Pliocene data are from this study (2.6–2.8 Ma) and from Badger et al. (2013b) (2.8–3.3 Ma). The lower panels show for the Pleistocene (c) and Pliocene (f) as red diamonds. The filled diamonds in panel (f) are from Badger et al. (2013b). The Pleistocene ice core data (Bereiter et al., 2015 and Table 1) are shown for comparison in panel (c). The drop in lith size from the Pliocene to Pleistocene is similar to what has been documented previously (Young, 1990). Outliers in panels (a) and (d) were calculated following the 1.5 rule in R (R Core Team, 2015).
Published low temporal resolution Pliocene records from Site 999 (Seki et al., 2010), using both the and palaeobarometers, show a pCO2 decrease at ∼2.8 Ma. However, this agreement relies on correcting the for changes in haptophyte cell size, which was based on a low temporal resolution lith size record (Seki et al., 2010). Changes in haptophyte cell size alter the volume to surface area ratio available for gaseous exchange and can therefore modify the fractionation recorded by (Popp et al., 1998). Our new record at Site 999 now spans 3.3–2.6 Ma at higher temporal resolution, supplementing data from Badger et al. (2013b). A lith size record has also been generated for the same samples used for for 3.3–2.6 Ma (Davis et al., 2013). We find no evidence to support the change in lith size applied by Seki et al. (2010) with lith size (and hence cell size) remaining stable across the primary pCO2 change at 2.8 Ma (Davis et al., 2013). Consequently, although our new record is of higher resolution than that of Seki et al. (2010), we no longer have any evidence for the cell size shift at 2.7 Ma (Fig. 4).
We compare our record with the records of Martínez-Botí et al. (2015) in Fig. 2. With the cell size correction now removed, the decrease in across the INHG, and the agreement of with , both now disappear (red symbols, Fig. 2b). As such, for this whole Pliocene interval (2.6–3.3 Ma) remains stable and low (mean ; 1σ min =228, max =286 µatm), whereas is on average higher and more variable (mean ; 1σ min =234, max =452 µatm).
In the Pleistocene, our record covers one complete glacial–interglacial (G-IG) cycle from 110 to 260 ka, encompassing MIS5–7, and the end of MIS8, and terminations II and III (open red diamonds; Fig. 2a). The record of Chalk et al. (2017) covers two G-IG cycles from the late Holocene to MIS8 (open blue circles; Fig. 2a). δ11Bplank closely tracks the rise and fall of pCO2 derived from ice cores (Chalk et al., 2017), with exhibiting similar values to atmospheric CO2 within uncertainty (Fig. 2a), and with only small deviations from ice core CO2 as a result of (i) the noise in the reconstruction and (ii) perhaps a small diagenetic effect on relating to periods of carbonate dissolution in portions of the core which show high foraminiferal fragmentation (e.g., MIS5d; Schmidt et al., 2006).
In contrast, is within error of the ice core data only during the interglacials when CO2 partial pressures are similar to those of the pre-industrial era. Crucially, clearly fails to record the lower pCO2 of the glacials, remaining at around 260 µatm throughout (mean ; Fig. 2a). This concentration of pCO2 is also very close to that recorded by in the Pliocene at this site (mean µatm; Fig. 2). Similar alkenone behaviour has also been observed in another, albeit lower-resolution, record from ODP Site 925 (Zhang et al., 2013; Fig. 2), where the remains unchanged during the Pleistocene (20–170 ka) and Pliocene.
Overall, these results suggest that, at least at these sites, the palaeobarometer does faithfully record atmospheric CO2 change, whereas the proxy is unable to reconstruct the low levels of atmospheric CO2 during the glacial. This suggests that, in its present and frequently applied form, is not accurately recording atmospheric CO2, and this could explain the discrepancy between the Pliocene and records. We further evaluate this by using regression analysis between ice core and the paired-proxy data (Fig. 5). levels are largely consistent with those determined from ice cores, clustering around the 1:1 line with a slope also close to 1 (0.95±0.13) (Fig. 5a), whereas variance in is strongly muted compared to that observed in the ice core data (Fig. 5b).
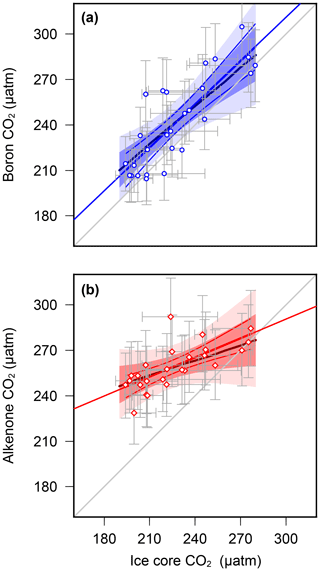
Figure 5Regression analyses of proxy-based pCO2 with ice core data (a) (Chalk et al., 2017) and (b) vs. ice core data (Bereiter et al., 2015 and Table 1) for MIS5–8, interpolated in the age domain. Regression lines (in red/blue) are linear fits with 68 % and 95 % confidence intervals, calculated by bootstrapping the uncertainties in proxy pCO2 (Monte Carlo method described in the methods section). Uncertainty in the ice core values is by estimated by applying a 3000 uncertainty in the age model during interpolation. Uncertainty envelopes considering data points alone (no bootstrap) are solid lines, with pmax regressions in the thicker, darker colours. A 1:1 line is shown in grey for comparison. Statistical calculations were performed in R (R Core Team, 2015).
As both cell size (Popp et al., 1998) and growth rate (Bidigare et al., 1997) can modify δ13Calk via the b term, we investigated whether either of these could explain the muted response of to atmospheric CO2. Haptophyte cell size can be estimated from their lith size, but as noted above, there is no evidence for significant changes in the Pliocene (Davis et al., 2013) nor is there evidence for any change across MIS5–8 (Fig. 4a). There is an overall reduction in mean lith size from the Pliocene to the Pleistocene (Fig. 4a, b), which could offset a long-term pCO2 decline and thus explain the apparent lack of difference between Pliocene and Pleistocene at Site 999 (Fig. 6). However, this longer-term reduction in lith size cannot explain the muted response to Pleistocene G-IG CO2 change.
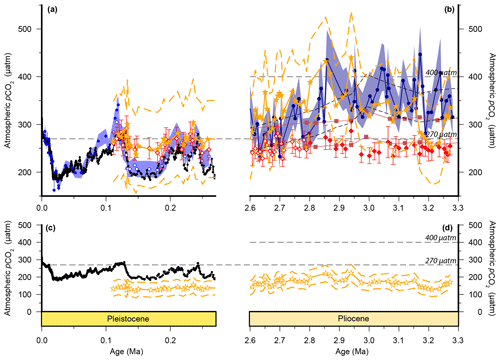
Figure 6Cell size corrections to . Ornamentation is the same as Fig. 1, with the addition of cell-size-corrected . The smaller liths than modern E. huxleyii across all of our records mean that a direct application of the method of Henderiks and Pagani (2007) results in substantially lower throughout (open orange stars; c, d). As the main interest is in the effect of the Plio-Pleistocene change in cell size we observe, we adjusted the b′ term so that matched our uncorrected record during the last interglacial (filled orange stars; a, b).
Growth rate is more difficult to reconstruct; most available proxy systems reconstruct phytoplankton or whole ecosystem productivity, rather than coccolithophorid growth rate. However, emerging trace metal datasets do suggest changing productivity on glacial–interglacial timescales at Site 999, with lower productivity in the glacial (Trumbo, 2015). If lower productivity is linked with a simultaneous reduction in growth rate, then it could explain some of the lack of signal in ; however, to reduce the sufficiently to overlap with ice core CO2 would require an order of magnitude reduction in growth rates during the glacial. This suggests that either our understanding of growth rate effects on is incorrect, or the estimation of cell size using preserved liths does not capture original cell size variations, or a combination of these or other factors leads to the rather muted trends in through the glacial–interglacial cycle.
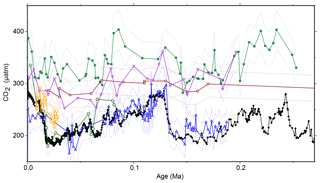
Figure 7Recalculated . Previous work (Jasper and Hayes, 1990; Jasper et al., 1994) calculated using a different model; here, we recalculate the earlier work using the modern methodology and Monte Carlo propagation applied to our other sites. All previous records have been recalculated using the same methodology as our new record, with some corrections and adjustments (for example, for growth rate or lith size) removed to allow direct comparisons. Records are from MANOP site C from the central equatorial Pacific (0∘57.2′ N, 138∘57.3′ W; filled green circles; Jasper et al., 1994), DSDP Site 619 in the Pigmy Basin, northern Gulf of Mexico (27∘11.6′ N, 91∘24.5′ W; open green circles; Jasper and Hayes, 1990), site 05PC-21 from the Sea of Japan (38.40∘ N, 131.55 ∘ E; open blue triangles; Bae et al., 2015), site NIOP464 in the Arabian Sea (22.15∘ N, 63.35∘ E; open orange hexagons; Palmer et al., 2010), site GeoB 1016-3 in the Angola Current (11.59∘ S, 11.70∘ E; inverted purple triangles; Andersen et al., 1999), and ODP Site 925 (4∘12.25′ N, 43∘29.33′ W; open dark red squares; Zhang et al., 2013). Ice core data are shown as filled black circles and lines (Bereiter et al., 2015 and Table 1). Dashed lines are 2σ uncertainties from Monte Carlo error propagation as described elsewhere in the text.
The failure of from these two sites to record the G-IG pCO2 variation also necessitates reassessment of earlier studies that were able to reconstruct such changes. For instance, whilst Jasper and Hayes (1990) replicated the CO2 change over the last 100 kyr of the Vostok ice core from Deep Sea Drilling Project (DSDP) Site 619 (Gulf of Mexico) and Bae et al. (2015) are able to replicate the ice core data at a site in the Sea of Japan, records from the Arabian Sea (Palmer et al., 2010), Angola Current (Andersen et al., 1999), and the equatorial Atlantic (Zhang et al., 2013) either fail to record ice core CO2 or require additional corrections to do so (Fig. 7). It may also be that at some sites, such as at equatorial Pacific MANOP (Manganese Nodule Project) site C (Figs. 1, 7), these records represent changing air–sea disequilibrium (Jasper et al., 1994). Two of these studies interpreted their data using a different εp relationship than later work; when these data are recalculated using the more recent model, the patterns remain unchanged (Fig. 7). What is more, in a global alkenone δ13C calibration study (Pagani et al., 2002) aimed at replicating Holocene atmospheric conditions, it was noted that low-latitude (subtropical) sites perform poorly, consistent with our observations. Considering this present study and previously published work, five out of seven late Pleistocene alkenone δ13C studies do not show the variations in pCO2 evident from contemporaneous ice core records (Figs. 2, 7).
Our Bayesian approach allows us to explore the proxy, as it was mathematically expressed by Bidigare et al. (1997) and subsequent authors, and test which variables may be responsible for causing the observed disagreement with the ice core and records given a largely invariant εp for the Pleistocene. Figure 8 illustrates the prior distributions of the input variables (blue) and an example posterior for the alkenone sample at 150 ka (red). As can be seen in this example, selecting only those simulations of that overlap with the ice core CO2 for this time interval shifts the distributions such that an agreement is found when b is lower than the prior, εf tends to be higher than the prior, and SST and CO2 disequilibrium are little different. Figure 9 shows the posterior median and 95 % distribution of b, εf, and SST for all the samples from the Pleistocene and Pliocene in time series. Patterns that emerge are illustrated in Fig. 10, where a negative relationship between pCO2 and posterior εf and a positive relationship between pCO2 and posterior b and SST are evident. For SST, it should also be noted that for the Pleistocene the posterior correlates well with the prior, while for the Pliocene it is significantly elevated (Fig. 10), perhaps suggesting a role for incorrect SST in driving some of the lack of Pliocene to Pleistocene change in observed (Fig. 2). This SST change would however need to be substantial and go beyond the ±2 ∘C we include in our uncertainty propagation, and would also potentially influence , further complicating this finding.
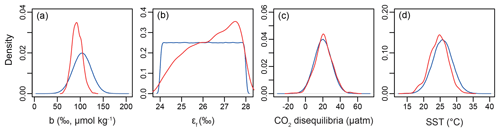
Figure 8Example of the Bayesian treatment of the proxy; the sample shown is 0.15 Ma from ODP Site 999. In all panels, the prior is shown in blue and the posterior in red. (a) The b term, (b) εf, (c) the extent of CO2 disequilibria, and (d) sea surface temperature.
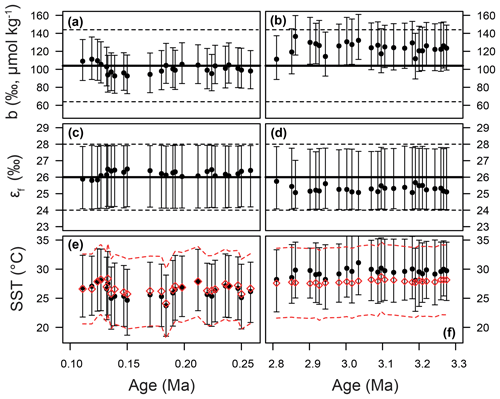
Figure 9Time series of priors and posteriors for the b term (a, b), εf (c, d), and SST (e, f). The Pleistocene is shown on the panels on the left and the Pliocene on the right. In panels (a–d), the mean of the prior distribution is shown as a thick black line. For the b term, 95 % of the input distribution is shown as a dotted line; for ε,f the total range is shown. See Fig. 7 for examples of these distributions as probability functions. For SST (e, f), the prior is shown as red diamonds, with 95 % of the distribution shown as the dashed lines. In all panels, the medians of the posterior distributions are shown as circles, with error bars encompassing 95 % of the range.
We recognize that the nature of the patterns we observe here is a function somewhat of the range used for each input term. The chosen ranges are however conservative, but realistic, assessments of the likely uncertainty associated with each term. For instance, b±40 encompasses the residual scatter around the relationship between b and [PO4] described by Pagani et al. (2005). In addition to pointing towards a potential underestimate of Pliocene SST with the proxy at ODP 999, this Bayesian treatment supports the assertion that the current understanding of the proxy is wanting and that the b term may not in fact capture the scaling of the relevant physiological parameters or those that are truly important. In particular, it appears that the physiological parameters packaged in the b term, and potentially the degree of fractionation upon fixation, εf, are themselves a function of CO2 or some parameter that correlates with CO2 (e.g., temperature, nutrients, growth rate).
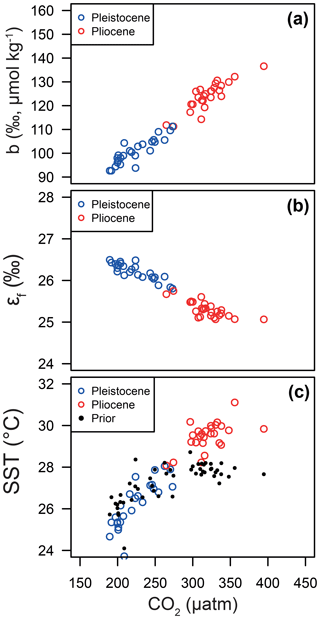
Figure 10Relationships between CO2 and (a) the b term, (b) εf and (c) SST. In each panel, the median of each posterior distribution is shown in red for the Pliocene and blue for the Pleistocene. Note that the CO2 for each data point is either from the ice core or for the Pleistocene and Pliocene, respectively. The linear patterns that emerge here essentially represent the relationships of the Bidigare et al. (1997) approach given our otherwise invariant εp.
As noted above, mean lith size is significantly different for the Pliocene and Pleistocene. A comparison of our posterior b and lith size does reveal a good correlation between these variables (Fig. 11; r2=0.52, p≪0.01), though this is largely, but not exclusively, a function of the mean change across the Plio-Pleistocene. Importantly, the observed relationship between b and lith size is very different from that described in Henderiks and Pagani (2007), suggesting that if lith size is important, our understanding, at least as laid out in Henderiks and Pagani (2007), is incorrect.
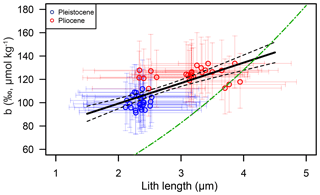
Figure 11Comparison between the posterior distribution for the Pliocene (red circles) and Pleistocene (blue circles) and the lith size correction of Henderiks and Pagani (2007) (green dot–dash line).
An alternative explanation however could be that the parameterization of physiological factors into the b term model is simply flawed in general, or is at least lacking important components. The dominant species producing alkenones in this part of the Caribbean today is Emiliania huxleyi (Winter et al., 2002). E. huxleyi first appeared 290 kyr ago but did not become the dominant Noelaerhabdaceae until ∼82 ka, when it began to outcompete the closely related Gephyrocapsa spp., which in turn took over from Reticulofenestra in the late Pliocene (Raffi et al., 2006; Gradstein et al., 2012). Both our alkenone records are therefore a composite of closely related but distinct Noelaerhabdaceaen species, with neither record dominated by E. huxleyi. We cannot rule out that there could be physiological differences between the extant E. huxleyi species and the alkenone producers for our record. However, the Site 925 record of the last glacial–interglacial cycle, which would been primarily sourced from E. huxleyi, is similarly flat, suggesting that species-specific biosynthesis differences are unlikely to be the whole story. The Reticulofenestra–Gephyrocapsa–Emiliania lineage has strong stratigraphic, morphological, and genetic support, with Emiliania and Gephyrocapsa only recently genetically diverging (Bendif et al., 2016). Likely, these taxa shared the same or similar ecologies. Recent experimental work has shown that this globally important species has evolved a carbon concentrating mechanism (CCM) to respond to limiting CO2 by upregulating genes at low DIC to maintain carbon requirements (Bach et al., 2013). CCMs result in a breakdown of the relationship between εp and CO2, as defined and calibrated by Bidigare et al. (1997). It has been thought that the increased expression of CCMs will cause εp values to decrease, due to the isotopic offset between CO2(aq) and and decreased carbon leakage from the cell (Zhang et al., 2013), effectively exacerbating the expected trend towards lower εp values at lower pCO2 and inconsistent with our observation of relatively stable εp values across G-IG cycles. However, CCMs appear to modulate carbon flow across cellular compartments (e.g., cytosol, chloroplast and calcification vesicle), and could also yield elevated rather than lower εp due to the concentrating of CO2 at the site of carbon fixation (Bolton and Stoll, 2013). Additionally, as temperature modulates resource allocation between biosynthesis and photosynthesis (Sett et al., 2014), CO2 optima are species specific and vary with temperature, which may explain why some sites in the region with different dominant haptophyte species are capable of recording G-IG changes whilst others struggle. Furthermore, it has been postulated that changes in carbonate chemistry affect the redox state inside E. huxleyi cells which subsequently causes a reorganization of carbon flux within and across cellular compartments (Rokitta et al., 2012). Such a redistribution of inorganic carbon amongst different pathways also likely influences εp and is currently not mechanistically represented by Bidigare et al. (1997) and other models.
Our data show that the classical application of the alkenone pCO2 proxy fails to capture glacial–interglacial changes observed in the ice cores. With increased confidence in supplied by that proxy's ability to capture Pleistocene pCO2 variability, our data also suggest that the discrepancy between and in the Pliocene may also be due to problems with . Emerging insights into coccolithophore CO2 allocation pathways and their sensitivity to CO2 and temperature, in conjunction with our inter-proxy comparisons, indicate that the long-standing proxy requires major revision and recalibration. If CCMs are preferentially more important for the alkenone palaeobarometer than growth rate, the muted alkenone palaeobarometer response may be limited to the low-CO2 world of the Plio-Pleistocene and particularly in tropical waters where CO2(aq) is especially low. By extension, this proxy (and interpretations based on it) likely retains utility at the higher CO2 levels typical of the early Cenozoic (and at high latitudes where CO2(aq) is high) where active carbon uptake is less likely (Zhang et al., 2013). This is especially true if haptophyte CCMs only evolved in the Late Miocene as a response to declining CO2 levels (Bolton and Stoll, 2013). Regardless, the discrepancy between and ice core CO2 records indicates that alkenone isotopes in several locations do not faithfully record atmospheric CO2 at relatively low, Plio-Pleistocene-like CO2 levels. Furthermore, the muted response of to [CO2(aq)] at lower concentrations calls into question the underlying basis of the high climate sensitivities previously reconstructed using this method in the Plio-Pleistocene (Pagani et al., 2009). This, coupled with further evidence of the fidelity of at Site 999, suggests that the climate sensitivities derived from (which are consistent with climate models used both in palaeoclimate and future climate projections) are more accurate (Martínez-Botí et al., 2015).
Data are archived on Pangaea (https://doi.pangaea.de/10.1594/PANGAEA.899353) (Badger et al., 2019).
The supplement related to this article is available online at: https://doi.org/10.5194/cp-15-539-2019-supplement.
MPSB and GLF conceived the study (conceptualization). MPSB, TBC, and GLF designed the methodology, carried out data collection, and analysed the data (formal analysis, investigation, methodology). PRB, SJG, HP, and AM performed data collection. PFS finalized the age model (investigation). MPSB wrote the manuscript and prepared figures (visualization, writing – original draft). RDP (PI), GLF, and DNS (CoIs) supervised the project and acquired funding (funding acquisition and supervision). All authors contributed to interpretation, writing, and reviewing the manuscript (writing – review and editing).
The authors declare that they have no conflict of interest.
This study used samples provided by the International Ocean Discovery Program (IODP). We thank Alex Hull and Gemma Bowler for laboratory work, Lisa Schönborn and Günter Meyer for technical assistance, Alison Kuhl and Ian Bull for research support, and Andy Milton at the University of Southampton for maintaining some of the mass spectrometers used in this study. This study was funded by NERC grant NE/H006273/1 to Richard D. Pancost, Daniela N. Schmidt and Gavin L. Foster (which supported Marcus P. S. Badger). We also acknowledge the ERC Award T-GRES and a Royal Society Wolfson Research Merit Award to Richard D. Pancost. Gavin L. Foster is also supported by a Royal Society Wolfson Research Merit Award. We thank Kirsty Edgar for comments on an early draft of the manuscript, the two anonymous reviewers of this submission, and reviewers through various rounds of review whose comments greatly improved the manuscript. We are grateful to Thomas Bauska for encouraging us to do better at referencing the ice core data, and John Jasper for discussion of the early days of the alkenone palaeobarometer.
This paper was edited by Luc Beaufort and reviewed by two anonymous referees.
Ahn, J. and Brook, E. J.: Siple Dome ice reveals two modes of millennial CO2 change during the last ice age, Nat. Commun., 5, 3723, https://doi.org/10.1038/ncomms4723, 2014.
Ahn, J., Brook, E. J., Mitchell, L., Rosen, J., McConnell, J. R., Taylor, K., Etheridge, D., and Rubino, M.: Atmospheric CO2 over the last 1000 years: A high-resolution record from the West Antarctic Ice Sheet (WAIS) Divide ice core, Global Biogeochem. Cy., 26, GB2027, https://doi.org/10.1029/2011GB004247, 2012.
Anagnostou, E., John, E. H., Edgar, K. M., Foster, G. L., Ridgwell, A., Inglis, G. N., Pancost, R. D., Lunt, D. J., and Pearson, P. N.: Changing atmospheric CO2 concentration was the primary driver of early Cenozoic climate, Nature, 533, 380–384, https://doi.org/10.1038/nature17423, 2016.
Andersen, N., Miiller, P. J., Kirsf, G., and Schneider, R. R.: Alkenone δ13C as a proxy for past pCO2 in surface waters: Results from the Late Quarternary Angola Current, 1999.
Bach, L. T., Mackinder, L. C. M., Schulz, K. G., Wheeler, G., Schroeder, D. C., Brownlee, C., and Riebesell, U.: Dissecting the impact of CO2 and pH on the mechanisms of photosynthesis and calcification in the coccolithophore Emiliania huxleyi., New Phytol., 199, 121–34, https://doi.org/10.1111/nph.12225, 2013.
Badger, M. P. S., Lear, C. H., Pancost, R. D., Foster, G. L., Bailey, T. R., Leng, M. J., and Abels, H. A.: CO2 drawdown following the middle Miocene expansion of the Antarctic Ice Sheet, Paleoceanography, 28, 42–53, https://doi.org/10.1002/palo.20015, 2013a.
Badger, M. P. S., Schmidt, D. N., Mackensen, A., and Pancost, R. D.: High-resolution alkenone palaeobarometry indicates relatively stable pCO2 during the Pliocene (3.3–2.8 Ma), Philos. T. R. Soc. A, 371, 20130094, https://doi.org/10.1098/rsta.2013.0094, 2013b.
Badger, M. P. S., Chalk, T. B., Foster, G. L., Bown, P. R., Gibbs, S. J., Sexton, P. F., Schmidt, D. N., Pälike, H., Mackensen, A., and Pancost, R. D.: Alkenone carbon isotopes, unsatutation measurements, coccolith size and stable planktic foraminifera carbon isotopes for estimation of atmospheric CO2 at ODP Site 999, PANGAEA, https://doi.org/10.1594/PANGAEA.899353, 2019.
Bae, S. W., Lee, K. E., and Kim, K.: Use of carbon isotopic composition of alkenone as a CO2 proxy in the East Sea/Japan Sea, Cont. Shelf Res., 107, 24–32, https://doi.org/10.1016/j.csr.2015.07.010, 2015.
Bartoli, G., Hönisch, B., and Zeebe, R. E.: Atmospheric CO2 decline during the Pliocene intensification of Northern Hemisphere glaciations, Paleoceanography, 26, PA4213, https://doi.org/10.1029/2010PA002055, 2011.
Bendif, E. M., Probert, I., Díaz-Rosas, F., Thomas, D., van den Engh, G., Young, J. R., and von Dassow, P.: Recent reticulate evolution in the ecologically dominant lineage of coccolithophores, Front. Microbiol., 7, 784, https://doi.org/10.3389/fmicb.2016.00784, 2016.
Bereiter, B., Lüthi, D., Siegrist, M., Schüpbach, S., Stocker, T. F., and Fischer, H.: Mode change of millennial CO2 variability during the last glacial cycle associated with a bipolar marine carbon seesaw, P. Natl. Acad. Sci. USA, 109, 9755–9760, https://doi.org/10.1073/pnas.1204069109, 2012.
Bereiter, B., Eggleston, S., Schmitt, J., Nehrbass-Ahles, C., Stocker, T. F., Fischer, H., Kipfstuhl, S., and Chappellaz, J.: Revision of the EPICA Dome C CO2 record from 800 to 600 kyr before present, Geophys. Res. Lett., 42, 542–549, https://doi.org/10.1002/2014GL061957, 2015.
Bidigare, R., Fluegge, A., Freeman, K. H., Hanson, K., Hayes, J. M., Hollander, D., Jasper, J. P., King, L. L., Laws, E., Milder, J., Millero, F. J., Pancost, R., Popp, B. N., Steinberg, P., and Wakeham, S. G.: Consistent fractionation of 13C in nature and in the laboratory: Growth-rate effects in some haptophyte algae, Global Biogeochem. Cy., 11, 279–292, https://doi.org/10.1029/96GB03939, 1997.
Bolton, C. T. and Stoll, H. M.: Late Miocene threshold response of marine algae to carbon dioxide limitation., Nature, 500, 558–562, https://doi.org/10.1038/nature12448, 2013.
Chalk, T. B., Hain, M. P., Foster, G. L., Rohling, E. J., Sexton, P. F., Badger, M. P. S., Cherry, S. G., Hasenfratz, A. P., Haug, G. H., Jaccard, S. L., Martínez-García, A., Pälike, H., Pancost, R. D., and Wilson, P. A.: Causes of ice age intensification across the Mid-Pleistocene Transition, P. Natl. Acad. Sci. USA, 114, 13114–13119, https://doi.org/10.1073/pnas.1702143114, 2017.
Davis, C. V., Badger, M. P. S., Bown, P. R., and Schmidt, D. N.: The response of calcifying plankton to climate change in the Pliocene, Biogeosciences, 10, 6131–6139, https://doi.org/10.5194/bg-10-6131-2013, 2013.
Delaney, M. L. and Boyle, E. A.: Li, Sr, Mg, and Na in foraminiferal calcite shells from laboratory culture , sediment traps, and sediment cores, Geochim. Cosmochim. Ac., 49, 1327–1341, 1985.
Dickson, A. G.: Thermodynamics of the dissociation of boric acid in synthetic seawater from 273.15 to 318.15 K, Deep-Sea Res., 37, 755–766, https://doi.org/10.1016/0198-0149(90)90004-F, 1990.
Evans, D. and Müller, W.: Deep time foraminifera Mg ∕ Ca paleothermometry: Nonlinear correction for secular change in seawater Mg ∕ Ca, Paleoceanography, 27, PA4205, https://doi.org/10.1029/2012PA002315, 2012.
Foster, G. L.: Seawater pH, pCO2 and [CO2-3] variations in the Caribbean Sea over the last 130 kyr: A boron isotope and B ∕ Ca study of planktic foraminifera, Earth Planet. Sc. Lett., 271, 254–266, https://doi.org/10.1016/j.epsl.2008.04.015, 2008.
Foster, G. L. and Sexton, P. F.: Enhanced carbon dioxide outgassing from the eastern equatorial Atlantic during the last glacial, Geology, 42, 1003–1006, https://doi.org/10.1130/G35806.1, 2014.
Foster, G. L., Hönisch, B., Paris, G., Dwyer, G. S., Rae, J. W. B. B., Elliott, T., Gaillardet, J., Hemming, N. G., Louvat, P., and Vengosh, A.: Interlaboratory comparison of boron isotope analyses of boric acid, seawater and marine CaCO3 by MC-ICPMS and NTIMS, Chem. Geol., 358, 1–14, https://doi.org/10.1016/j.chemgeo.2013.08.027, 2013.
Foster, G. L., Royer, D. L., and Lunt, D. J.: Future climate forcing potentially without precedent in the last 420 million years, Nat. Commun., 8, 14845, https://doi.org/10.1038/ncomms14845, 2017.
Gattuso, J.-P., Epitalalon, J.-M., and Lavigne, H.: Seacarb: Seawater Carbonate Chemistry, R package version 3.0.8, 2015.
Gibbs, S. J., Poulton, A. J., Bown, P. R., Daniels, C. J., Hopkins, J., Young, J. R., Jones, H. L., Thiemann, G. J., O'Dea, S. A., and Newsam, C.: Species-specific growth response of coccolithophores to Palaeocene–Eocene environmental change, Nat. Geosci., 6, 218–222, https://doi.org/10.1038/ngeo1719, 2013.
Gradstein, F., Ogg, J., Schmitz, M., and Ogg, G.: The Geologic Time Scale 2012, 1st ed., edited by: Gradstein, F., Ogg, J., Schmitz, M., and Ogg, G., Elsevier, Oxford, UK, 2012.
Hemming, N. G. and Hanson, G. N.: Boron isotopic composition and concentration in modern marine carbonates, Geochim. Cosmochim. Ac., 56, 537–543, https://doi.org/10.1016/0016-7037(92)90151-8, 1992.
Henderiks, J.: Coccolithophore size rules – Reconstructing ancient cell geometry and cellular calcite quota from fossil coccoliths, Mar. Micropaleontol., 67, 143–154, https://doi.org/10.1016/j.marmicro.2008.01.005, 2008.
Henderiks, J. and Pagani, M.: Refining ancient carbon dioxide estimates: Significance of coccolithophore cell size for alkenone-based pCO2 records, Paleoceanography, 22, PA3202, https://doi.org/10.1029/2006PA001399, 2007.
Henehan, M. J., Rae, J. W. B. B., Foster, G. L., Erez, J., Prentice, K. C., Kucera, M., Bostock, H. C., Martínez-Botí, M. A., Milton, J. A., Wilson, P. A., Marshall, B. J., and Elliott, T.: Calibration of the boron isotope proxy in the planktonic foraminifera Globigerinoides ruber for use in palaeo-CO2 reconstruction, Earth Planet. Sc. Lett., 364, 111–122, https://doi.org/10.1016/j.epsl.2012.12.029, 2013.
Hönisch, B. and Hemming, N. G.: Surface ocean pH response to variations in pCO2 through two full glacial cycles, Earth Planet. Sc. Lett., 236, 305–314, https://doi.org/10.1016/j.epsl.2005.04.027, 2005.
Jasper, J. and Hayes, J.: A carbon isotope record of CO2 levels during the late Quaternary, Nature, 347, 462–464, available at: https://www.nature.com/articles/347462a0 (last access: 12 January 2015), 1990.
Jasper, J., Hayes, J., Mix, A., and Prahl, F.: Photosynthetic fractionation of 13C and concentrations of dissolved CO2 in the central equatorial Pacific during the last 255 000 years, Paleoceanography, 9, 781–798, https://doi.org/10.1029/94PA02116, 1994.
Klochko, K., Kaufman, A. J., Yao, W., Byrne, R. H., and Tossell, J. A.: Experimental measurement of boron isotope fractionation in seawater, Earth Planet. Sc. Lett., 248, 276–285, https://doi.org/10.1016/j.epsl.2006.05.034, 2006.
Lacis, A. A., Schmidt, G. A., Rind, D., and Ruedy, R. A.: Atmospheric CO2: Principal Control Knob Governing Earth's Temperature, Science, 330, 356–359, https://doi.org/10.1126/science.1190653, 2010.
Laws, E. A., Bidigare, R. R., and Popp, B. N.: Effect of growth rate and CO2 concentration on carbon isotopic fractionation by the marine diatom Phaeodactylum tricornutum, Limnol. Oceanogr., 42, 1552–1560, https://doi.org/10.4319/lo.1997.42.7.1552, 1997.
Lisiecki, L. E. and Raymo, M. E.: A Pliocene-Pleistocene stack of 57 globally distributed benthic δ18O records, Paleoceanography, 20, PA1003, https://doi.org/10.1029/2004PA001071, 2005.
MacFarling Meure, C., Etheridge, D., Trudinger, C., Steele, P., Langenfelds, R., van Ommen, T., Smith, A., and Elkins, J.: Law Dome CO2, CH4 and N2O ice core records extended to 2000 years BP, Geophys. Res. Lett., 33, L14810, https://doi.org/10.1029/2006gl026152, 2006.
Marcott, S. A., Bauska, T. K., Buizert, C., Steig, E. J., Rosen, J. L., Cuffey, K. M., Fudge, T. J., Severinghaus, J. P., Ahn, J., Kalk, M. L., McConnell, J. R., Sowers, T., Taylor, K. C., White, J. W. C., and Brook, E. J.: Centennial-scale changes in the global carbon cycle during the last deglaciation, Nature, 514, 616–619, https://doi.org/10.1038/nature13799, 2014.
Martínez-Botí, M. A., Foster, G. L., Chalk, T. B., Rohling, E. J., Sexton, P. F., Lunt, D. J., Pancost, R. D., Badger, M. P. S., and Schmidt, D. N.: Plio-Pleistocene climate sensitivity evaluated using high-resolution CO2 records, Nature, 518, 49–54, https://doi.org/10.1038/nature14145, 2015.
Monnin, E., Indermuhle, A., Dallenbach, A., Fluckiger, J., Stauffer, B., Stocker, T. F., Raynaud, D., and Barnola, J. M.: Atmospheric CO2 concentrations over the last glacial termination, Science, 291, 112–114, https://doi.org/10.1126/science.291.5501.112, 2001.
Monnin, E., Steig, E. J., Siegenthaler, U., Kawamura, K., Schwander, J., Stauffer, B., Stocker, T. F., Morse, D. L., Barnola, J.-M., Bellier, B., Raynaud, D., and Fischer, H.: Evidence for substantial accumulation rate variability in Antarctica during the Holocene, through synchronization of CO2 in the Taylor Dome, Dome C and DML ice cores, Earth Planet. Sc. Lett., 224, 45–54, https://doi.org/10.1016/j.epsl.2004.05.007, 2004.
Müller, P., Kirst, G., Ruhland, G., von Storch, I., and Rosell-Melé, A.: Calibration of the alkenone paleotemperature index based on core-tops from the eastern South Atlantic and the global ocean (60∘ N–60∘ S), Geochim. Cosmochim. Ac., 62, 1757–1772, available at: https://www.sciencedirect.com/science/article/pii/S0016703798000970 (last access: 13 January 2015), 1998.
Pagani, M., Freeman, K. H., Ohkouchi, N., and Caldeira, K.: Comparison of water column [CO2aq] with sedimentary alkenone-based estimates: A test of the alkenone-CO2 proxy, Paleoceanography, 17, 21-1–21-12, https://doi.org/10.1029/2002PA000756, 2002.
Pagani, M., Zachos, J. C., Freeman, K. H., Tipple, B., and Bohaty, S.: Marked decline in atmospheric carbon dioxide concentrations during the Paleogene., Science, 309, 600–603, https://doi.org/10.1126/science.1110063, 2005.
Pagani, M., Liu, Z., LaRiviere, J., and Ravelo, A. C.: High Earth-system climate sensitivity determined from Pliocene carbon dioxide concentrations, Nat. Geosci., 3, 27–30, https://doi.org/10.1038/ngeo724, 2009.
Pagani, M., Huber, M., Liu, Z., Bohaty, S. M., Henderiks, J., Sijp, W., Krishnan, S., and DeConto, R. M.: The role of carbon dioxide during the onset of Antarctic glaciation., Science, 334, 1261–1264, https://doi.org/10.1126/science.1203909, 2011.
Paillard, D., Labeyrie, L., and Yiou, P.: Macintosh Program performs time-series analysis, Eos T. Am. Geophys. Un., 77, 379–379, https://doi.org/10.1029/96EO00259, 1996.
PALAEOSENS: Making sense of palaeoclimate sensitivity, Nature, 491, 683–691, https://doi.org/10.1038/nature11574, 2012.
Palmer, M. R. R., Brummer, G. J. J., Cooper, M. J. J., Elderfield, H., Greaves, M. J. J., Reichart, G. J. J., Schouten, S., and Yu, J. M. M.: Multi-proxy reconstruction of surface water pCO2 in the northern Arabian Sea since 29 ka, Earth Planet. Sc. Lett., 295, 49–57, https://doi.org/10.1016/j.epsl.2010.03.023, 2010.
Pearson, P. N., Foster, G. L., and Wade, B. S.: Atmospheric carbon dioxide through the Eocene-Oligocene climate transition, Nature, 461, 1110–1113, https://doi.org/10.1038/nature08447, 2009.
Petit, J. R., Jouzel, J., Raynaud, D., Barkov, N. I., Barnola, J.-M., Basile, I., Bender, M., Chappellaz, J., Davis, M., Delaygue, G., Delmotte, M., Kotlyakov, V. M., Legrand, M., Lipenkov, V. Y., Lorius, C., Pepin, K., Ritz, C., Saltzman, E., and Stievenard, M.: Climate and atmospheric history of the past 420 000 years from the Vostok ice core, Antarctica, Nature, 399, 429–436, available at: https://www.nature.com/articles/20859 (last access: 12 January 2015), 1999.
Popp, B., Laws, E., Bidigare, R., Dore, J., Hanson, K., and Wakeham, S. G.: Effect of phytoplankton cell geometry on carbon isotopic fractionation, Geochim. Cosmochim. Ac., 62, 67–77, available at: https://www.sciencedirect.com/science/article/pii/S0016703797003335 (last access: 12 January 2015), 1998.
Rae, J. W. B. B., Foster, G. L., Schmidt, D. N., and Elliott, T.: Boron isotopes and B/Ca in benthic foraminifera: Proxies for the deep ocean carbonate system, Earth Planet. Sc. Lett., 302, 403–413, https://doi.org/10.1016/j.epsl.2010.12.034, 2011.
Raffi, I., Backman, J., Fornaciari, E., Pälike, H., Rio, D., Lourens, L., and Hilgen, F.: A review of calcareous nannofossil astrobiochronology encompassing the past 25 million years?, Quaternary Sci. Rev., 25, 3113–3137, https://doi.org/10.1016/j.quascirev.2006.07.007, 2006.
R Core Team: R: A language and environment for statistical computing, R Foundation for Statistical Computing, Vienna, Austria, available at: https://www.R-project.org/ (last access: 21 March 2019) 2015.
Rokitta, S. D., John, U., and Rost, B.: Ocean Acidification Affects Redox-Balance and Ion-Homeostasis in the Life-Cycle Stages of Emiliania huxleyi, edited by: Dupont, S., PLoS One, 7, e52212, https://doi.org/10.1371/journal.pone.0052212, 2012.
Rubino, M., Etheridge, D. M., Trudinger, C. M., Allison, C. E., Battle, M. O., Langenfelds, R. L., Steele, L. P., Curran, M., Bender, M., White, J. W. C., Jenk, T. M., Blunier, T., and Francey, R. J.: A revised 1000 year atmospheric δ13C-CO2 record from Law Dome and South Pole, Antarctica, J. Geophys. Res.-Atmos., 118, 8482–8499, https://doi.org/10.1002/jgrd.50668, 2013.
Sanyal, A. and Hemming, N.: Oceanic pH control on the boron isotopic composition of foraminifera: evidence from culture experiments, Paleoceanography, 11, 513–517, https://doi.org/10.1029/96PA01858, 1996.
Sanyal, A., Hemming, N., Hanson, G., and Broecker, W.: Evidence for a higher pH in the glacial ocean from boron isotopes in foraminifera, Nature, 373, 234–236, available at: https://websites.pmc.ucsc.edu/~apaytan/290A_Winter2014/pdfs/B isotopes Jn 24-1.pdf (last access: 12 January 2015), 1995.
Schmidt, M. W., Vautravers, M. J., and Spero, H. J.: Western Caribbean sea surface temperatures during the late Quaternary, Geochem. Geophy. Geosy., 7, Q02P10, https://doi.org/10.1029/2005GC000957, 2006.
Schneider, R., Schmitt, J., Köhler, P., Joos, F., and Fischer, H.: A reconstruction of atmospheric carbon dioxide and its stable carbon isotopic composition from the penultimate glacial maximum to the last glacial inception, Clim. Past, 9, 2507–2523, https://doi.org/10.5194/cp-9-2507-2013, 2013.
Seki, O., Foster, G. L., Schmidt, D. N., Mackensen, A., Kawamura, K., and Pancost, R. D.: Alkenone and boron-based Pliocene pCO2 records, Earth Planet. Sc. Lett., 292, 201–211, https://doi.org/10.1016/j.epsl.2010.01.037, 2010.
Sett, S., Bach, L. T., Schulz, K. G., Koch-Klavsen, S., Lebrato, M., and Riebesell, U.: Temperature modulates coccolithophorid sensitivity of growth, photosynthesis and calcification to increasing seawater pCO2, PLoS One, 9, e88308, https://doi.org/10.1371/journal.pone.0088308, 2014.
Sheward, R. M., Poulton, A. J., Gibbs, S. J., Daniels, C. J., and Bown, P. R.: Physiology regulates the relationship between coccosphere geometry and growth phase in coccolithophores, Biogeosciences, 14, 1493–1509, https://doi.org/10.5194/bg-14-1493-2017, 2017.
Sosdian, S. M., Greenop, R., Hain, M. P., Foster, G. L., Pearson, P. N., and Lear, C. H.: Constraining the evolution of Neogene ocean carbonate chemistry using the boron isotope pH proxy, Earth Planet. Sc. Lett., 498, 362–376, https://doi.org/10.1016/J.EPSL.2018.06.017, 2018.
Super, J. R., Thomas, E., Pagani, M., Huber, M., Brien, C. O. and Hull, P. M.: North Atlantic temperature and pCO2 coupling in the early-middle Miocene, Geology, 46, 519–522, https://doi.org/10.1130/G40228.1, 2018.
Takahashi, T., Sutherland, S. C., Wanninkhof, R., Sweeney, C., Feely, R. a., Chipman, D. W., Hales, B., Friederich, G., Chavez, F., Sabine, C., Watson, A., Bakker, D. C. E. E., Schuster, U., Metzl, N., Yoshikawa-Inoue, H., Ishii, M., Midorikawa, T., Nojiri, Y., Körtzinger, A., Steinhoff, T., Hoppema, M., Olafsson, J., Arnarson, T. S., Tilbrook, B., Johannessen, T., Olsen, A., Bellerby, R., Wong, C. S. S., Delille, B., Bates, N. R. R., and de Baar, H. J. W. W.: Climatological mean and decadal change in surface ocean pCO2, and net sea–air CO2 flux over the global oceans, Deep-Sea Res. Pt. II, 56, 554–577, https://doi.org/10.1016/j.dsr2.2008.12.009, 2009.
Trumbo, S. K.: Marine Export Productivity and the Demise of the Central American Seaway, UC San Diego, available at: https://escholarship.org/uc/item/83f2w736 (last access: 21 March 2019), 2015.
Winter, A., Rost, B., Hilbrecht, H., and Elbrächter, M.: Vertical and horizontal distribution of coccolithophores in the Caribbean Sea, Geo-Mar. Lett., 22, 150–161, https://doi.org/10.1007/s00367-002-0108-8, 2002.
Young, J.: Size variation of Neogene Reticulofenestra coccoliths from Indian Ocean DSDP Cores, J. Micropalaeontol., 9, 71–85, https://doi.org/10.1144/jm.9.1.71, 1990.
Zhang, Y. G., Pagani, M., Liu, Z., Bohaty, S. M., and Deconto, R.: A 40-million-year history of atmospheric CO2, Philos. T. R. Soc. A., 371, 20130096, https://doi.org/10.1098/rsta.2013.0096, 2013.