the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Assessing the robustness of Antarctic temperature reconstructions over the past 2 millennia using pseudoproxy and data assimilation experiments
François Klein
Nerilie J. Abram
Mark A. J. Curran
Hugues Goosse
Sentia Goursaud
Valérie Masson-Delmotte
Andrew Moy
Raphael Neukom
Anaïs Orsi
Jesper Sjolte
Nathan Steiger
Barbara Stenni
Martin Werner
The Antarctic temperature changes over the past millennia remain more uncertain than in many other continental regions. This has several origins: (1) the number of high-resolution ice cores is small, in particular on the East Antarctic plateau and in some coastal areas in East Antarctica; (2) the short and spatially sparse instrumental records limit the calibration period for reconstructions and the assessment of the methodologies; (3) the link between isotope records from ice cores and local climate is usually complex and dependent on the spatial scales and timescales investigated. Here, we use climate model results, pseudoproxy experiments and data assimilation experiments to assess the potential for reconstructing the Antarctic temperature over the last 2 millennia based on a new database of stable oxygen isotopes in ice cores compiled in the framework of Antarctica2k (Stenni et al., 2017). The well-known covariance between δ18O and temperature is reproduced in the two isotope-enabled models used (ECHAM5/MPI-OM and ECHAM5-wiso), but is generally weak over the different Antarctic regions, limiting the skill of the reconstructions. Furthermore, the strength of the link displays large variations over the past millennium, further affecting the potential skill of temperature reconstructions based on statistical methods which rely on the assumption that the last decades are a good estimate for longer temperature reconstructions. Using a data assimilation technique allows, in theory, for changes in the δ18O–temperature link through time and space to be taken into account. Pseudoproxy experiments confirm the benefits of using data assimilation methods instead of statistical methods that provide reconstructions with unrealistic variances in some Antarctic subregions. They also confirm that the relatively weak link between both variables leads to a limited potential for reconstructing temperature based on δ18O. However, the reconstruction skill is higher and more uniform among reconstruction methods when the reconstruction target is the Antarctic as a whole rather than smaller Antarctic subregions. This consistency between the methods at the large scale is also observed when reconstructing temperature based on the real δ18O regional composites of Stenni et al. (2017). In this case, temperature reconstructions based on data assimilation confirm the long-term cooling over Antarctica during the last millennium, and the later onset of anthropogenic warming compared with the simulations without data assimilation, which is especially visible in West Antarctica. Data assimilation also allows for models and direct observations to be reconciled by reproducing the east–west contrast in the recent temperature trends. This recent warming pattern is likely mostly driven by internal variability given the large spread of individual Paleoclimate Modelling Intercomparison Project (PMIP)/Coupled Model Intercomparison Project (CMIP) model realizations in simulating it. As in the pseudoproxy framework, the reconstruction methods perform differently at the subregional scale, especially in terms of the variance of the time series produced. While the potential benefits of using a data assimilation method instead of a statistical method have been highlighted in a pseudoproxy framework, the instrumental series are too short to confirm this in a realistic setup.
- Article
(11325 KB) -
Supplement
(800 KB) - BibTeX
- EndNote
Over the last few decades, the Antarctic Peninsula and West Antarctica have experienced a strong warming, while no significant temperature trend has been recorded in East Antarctica (Nicolas and Bromwich, 2014; Jones et al., 2016). The attribution of the causes of these changes is complicated by the large interannual to multi-decadal variability that characterizes the Antarctic climate (Schneider et al., 2006; Goosse et al., 2012; Jones et al., 2016), stressing the importance of considering a longer period to put the recent changes in a wider perspective. This is not possible using the instrumental record that generally only goes back to the late 1950s in Antarctica (Nicolas and Bromwich, 2014; Jones et al., 2016). Nevertheless, temperature information on a longer timescale can be inferred from stable isotope ratios of oxygen and hydrogen recorded in ice cores (e.g., Dansgaard, 1964; Jouzel, 2003; Masson-Delmotte et al., 2006).
However, the spatial coverage of high-resolution (annual to decadal) cores is uneven with a very small number of cores in dry regions such as the central East Antarctic plateau (Stenni et al., 2017), and in some coastal areas such as Adélie Land (Goursaud et al., 2017). In addition to the limitations related to the number and distribution of the cores, there are several sources of uncertainty in reconstructions based on these data. The period available to calibrate the records is very short due to the limited availability of instrumental records. In addition, it has been long established that the relationship between isotopes and surface temperature may differ spatially and temporally (e.g., Jouzel et al., 1997) as a result of changes in the origin of moisture, atmospheric transport pathways (e.g., Schlosser et al., 2004), or precipitation seasonality (e.g., Sime et al., 2008; Masson-Delmotte et al., 2008; Sodemann and Stohl, 2009). Finally, non-climatic noise related to postdepositional effects associated, for instance, with wind scouring and water vapor also adds to the challenge of interpreting the ice-core signals (e.g., Ekaykin et al., 2014; Ritter et al., 2016; Casado et al., 2016).
Thus, individual ice-core records may be affected by non-climatic, very local processes. Combining individual records in a given location or region has the potential to improve the signal-to-noise ratio (SNR). This was done at the continental scale in Goosse et al. (2012), where a composite of last millennium Antarctic temperature was presented. This composite is based on the average of seven temperature records derived from isotope measurements in ice cores, and shows a weak multi-centennial cooling trend over the preindustrial period followed by a warming after 1850 CE. A similar last millennium cooling is observed in the reconstruction of the PAGES 2k Consortium (2013) which is based on a composite-plus-scaling (CPS) approach (e.g., Schneider et al., 2006), using 11 records, although no clear recent warming is observed in this reconstruction.
Those continental-scale trends based on a limited number of records actually mask important spatial variations as shown in Stenni et al. (2017). Using a new database compiled in the framework of the PAGES Antarctica2k working group that contains 112 isotopic records, Stenni et al. (2017) produced temperature reconstructions over the last 2 millennia on both regional and continental scales. Those reconstructions confirm the last millennium cooling over Antarctica, which is strongest in West Antarctica, and show no evident warming during the last century at the continent scale, despite the significant positive temperature trends observed in the Antarctic Peninsula, the West Antarctic Ice Sheet (WAIS) and coastal Dronning Maud Land (DML).
In contrast, climate model simulations performed in the framework of the third phase of the Past Model Intercomparison Project (PMIP3; Otto-Bliesner et al., 2009) and the fifth phase of the Coupled Model Intercomparison Project (CMIP5; Taylor et al., 2012) show a general twentieth century warming over Antarctica due to anthropogenic forcing (Goosse et al., 2012; PAGES 2k-PMIP3 group, 2015). As pointed out by Jones et al. (2016), this model–data mismatch at the continental scale suggests that the CMIP5 models overestimate the forced response, that the forced changes in the real world are overwhelmed by natural variability, or a combination of both of these factors. Part of the disagreement may also be due to observational gaps and uncertainties in regional temperature estimates.
To complement the limited information available from direct temperature observations, it is necessary to extract as much reliable temperature information as possible from ice-core water stable isotope records. In this context, our goal here is to assess the robustness of Antarctic temperature reconstructions over the last 2 millennia presented in Stenni et al. (2017), focusing on the potential impact of spatial and temporal changes in the δ18O–surface temperature relationship on the reconstruction skill. This is achieved by means of model results analysis, pseudoproxy experiments and data assimilation.
As our study is based on model results, it is important to first characterize the similarities and differences between simulated, reconstructed and observed temperature over the last millennium, at the regional scale. The simulated temperature products are derived from model simulations following the PMIP3 and CMIP5 protocols (Schmidt et al., 2011; Taylor et al., 2012), and from simulations from two isotope-enabled climate models, ECHAM5/MPI-OM (Werner et al., 2016) and ECHAM5-wiso (Werner et al., 2011). These simulated temperatures are compared to the regional temperature reconstructions from Stenni et al. (2017), and to the instrumental-based reconstruction produced by Nicolas and Bromwich (2014), covering the recent period from 1958 CE, and defined at a 60 km resolution.
The potential for reconstructing surface temperature based on water stable isotopes is then assessed in two stages. First, via the study of the stability of the relationship between these two variables in the model world over the last millennium using the results of the ECHAM5/MPI-OM and ECHAM5-wiso models, and second, using pseudoproxy experiments. Pseudoproxy experiments consist of utilizing climate model results to evaluate the performance of paleoclimate reconstruction methods in a flexible and controlled framework (e.g., Smerdon, 2012). The methodologies applied to obtain the paleoclimate reconstructions are applied in the model world, where all variables are known, allowing for the precise and quantitative assessment of the skill of the reconstructions. The resulting findings may not be fully valid for real-world implications, due to model biases, unrealistic pseudoproxies or the dependency of the pseudoproxy on the model from which they originate (Smerdon et al., 2016). However, the lack of real-world data, especially in Antarctica, limits the extent of (or even prevents) the evaluation of reconstruction methods, emphasizing the advantages of using pseudoproxy experiments. The complexity of the δ18O–temperature relationship, which potentially limits the reconstruction skill, further stresses the importance of using such experiments. Here, the pseudoproxies are derived from an ECHAM5/MPI-OM simulation covering the 800–1999 CE period (Sjolte et al., 2018). These pseudoproxies are used as input data for the different statistical methods utilized in Stenni et al. (2017) for reconstructing temperature based on δ18O, as well as for data assimilation experiments.
When applied to paleoclimatology, data assimilation aims at combining information from model results and proxy-based reconstructions to find estimates of past climate changes (e.g., Widmann et al., 2010; Hakim et al., 2016). Reconstructing temperature based on δ18O data using a data assimilation method potentially has several advantages compared with using statistical methods. First, data assimilation does not rely on a constant and stable relationship between δ18O and surface temperature, unlike the statistical methods used in Stenni et al. (2017). Second, data assimilation takes the spatial dependency of temperature into account which is not the case for the reconstructions of Stenni et al. (2017). Third, if a skilful reconstruction can be achieved, climate variables other than temperature can be reconstructed without any spatial or temporal gap, which may help interpret the signals present in ice-core records, although this falls outside of the scope of the present study.
After the assessment of the statistical and data assimilation methods in the light of the pseudoproxy experiments, the real temperature reconstructions over the last 2 millennia based on the new δ18O database presented in Stenni et al. (2017) are compared. Comparing the output of the different reconstruction methods allows for an assessment of how robust the reconstructions are, and how sensitive they are to the specificities of the methods. Particular focus is placed on whether the simulated spatial pattern of recent temperature trends and the measured and observed trends can be reconciled through data assimilation, or whether there is a fundamental discrepancy between model and data in this regard.
This study is structured as follows. The climate model simulations, the water stable isotopes records and the different reconstruction methods are described in Sect. 2. The simulated and reconstructed last millennium temperature changes are analyzed in Sect. 3, and compared to instrumental records over the recent past. The potential for reconstructing surface temperature based on water stable isotopes is assessed in Sect. 4, focusing on the δ18O–surface temperature relationship and pseudoproxy experiments. Finally, the temperature reconstructions based on various reconstructions methods are presented and discussed in Sect. 5, followed by the conclusion.
2.1 Climate model simulations
Simulations performed with two isotope-enabled general circulation models (GCMs), ECHAM5/MPI-OM (Werner et al., 2016) and ECHAM5-wiso (Werner et al., 2011), are analyzed and used as a basis for the data assimilation experiments. ECHAM5/MPI-OM is a fully coupled ocean–atmosphere–sea-ice–land surface GCM. The simulation used in the present study covers the 800–1999 CE period with a horizontal resolution of 3.75∘ × 3.75∘ (Sjolte et al., 2018). It is driven through the past millennium by both natural and anthropogenic forcings as described in Sjolte et al. (2018). ECHAM5-wiso is an atmosphere-only GCM. The run employed in this study was performed by Steiger et al. (2017) and spans the years from 1871 to 2011 CE at 1.125∘ spatial resolution. It is forced through this period by monthly historical sea ice and sea surface temperatures (SST) from the Met Office Hadley Centre's sea ice and sea surface temperature data set (Rayner et al., 2003). The evaluation of these simulations against recent observations (Global Network of Isotopes in Precipitation, GNIP, IAEA/WMO, 2018) shows a relatively good agreement between simulated and observed oxygen ratios in precipitation regarding various diagnostics, including spatial patterns, magnitude of the changes, and δ18O–surface temperature relationships (Werner et al., 2016; Steiger et al., 2017). Focusing on Antarctica, ECHAM5/MPI-OM and ECHAM5-wiso simulate similar absolute values and spatial patterns of δ18O (Fig. S1 in the Supplement) to another ECHAM5-wiso simulation nudged with ERA-Interim atmospheric reanalyses data (Dee et al., 2011) over the 1979–2013 CE period (Goursaud et al., 2018). This latter simulation was extensively studied in Goursaud et al. (2018), where they concluded that, despite an overall underestimation of isotopic depletion by ECHAM5-wiso compared with a collection of water stable isotope measurements, the model correctly captured the spatial gradient of annually averaged δ18O data; this justifies the use of the model to study water stable isotopes in Antarctic precipitation, and gives confidence regarding the use of the longer simulations from ECHAM5/MPI-OM and ECHAM5-wiso for our analysis. In this study, model outputs are processed to calculate precipitation-weighted δ18O at the temporal resolution of the corresponding analysis for comparison with ice-core records.
In addition to ECHAM results, last millennium temperature fields simulated by six models following the PMIP3 (Otto-Bliesner et al., 2009) and CMIP5 (Taylor et al., 2012) protocols are analyzed in Sect. 3. Details on models used in this study are listed in Table 1. See Klein et al. (2016) for a description of the forcings driving these simulations.
Werner et al. (2016)Werner et al. (2011)Gent et al. (2011)Otto-Bliesner et al. (2016)Schmidt et al. (2014)Dufresne et al. (2013)Stevens et al. (2013)Wu et al. (2014)2.2 Water stable isotope records
The data used in this study to assess and constrain model results consists of composites of water stable isotopes for seven climatically distinct regions covering the Antarctic continent: the East Antarctic plateau, Wilkes Land coast, Weddell Sea coast, the Antarctic Peninsula, WAIS, Victoria Land–Ross Sea and DML coast (Stenni et al., 2017). These regions, which are described in detail in Stenni et al. (2017), display relatively homogeneous characteristics in terms of regional climate and snow deposition processes, and were validated and refined by spatial correlation of temperature using the instrumental-based reconstruction of Nicolas and Bromwich (2014). The regional composites are based on 112 individual ice-core water stable isotope records compiled in the framework of the PAGES Antarctica2k working group. Most of these records are oxygen isotope ratios, and those that are deuterium isotopes (δD) have been converted to a δ18O equivalent by dividing by 8, which represents the slope of the global mean meteoric relationship of oxygen and deuterium isotopes in precipitation (Stenni et al., 2017).
Most individual records have a data resolution ranging from 0.025 to 5 years. In order to limit the influence of non-climatic noise induced by postdepositional processes (e.g., Münch et al., 2017; Jones et al., 2017; Laepple et al., 2018), they were all 5-year averaged for reconstructing the last 2 centuries and 10-year averaged for reconstructing the last 2 millennia. This lower temporal resolution also limits the potential influence of small age uncertainties. The spatial distribution of the individual records is strongly heterogeneous (Stenni et al., 2017). To avoid an overrepresentation in the composites of the areas with a relatively higher density of ice-core networks compared with other regions, the number of records was reduced based on a 2∘ latitude × 10∘ longitude grid in which multiple records falling into the same grid cell were averaged. This cut the number of individual series down to 40 with the following distribution: 15 for the East Antarctic plateau, 2 for the Wilkes Land coast, 1 for the Weddell Sea coast, 4 for the Antarctic Peninsula, 10 for the WAIS, 3 for the Victoria Land–Ross Sea sector and 5 for the DML coast. In Stenni et al. (2017), different methods were used to produce the seven composites from the preprocessed data, including a simple average per subregion, and weighted averages based on the temperature regressions of each site and the relevant region. Here, the composites using the latter method are used. However, all methods give consistent δ18O trends and variability.
2.3 Data assimilation method
The data assimilation method used to perform the temperature reconstruction is based on a particle filter (e.g., van Leeuwen, 2009) that is applied off-line, meaning that data assimilation makes use of an existing and fixed ensemble of simulated climate states. Off-line data assimilation methods contrast with online methods where the ensemble is generated sequentially, depending on the analysis made via the data assimilation process on the previous time step. An online method can theoretically outperform an off-line method if the state of the system at one particular time significantly influences its subsequent evolution between two assimilation steps, as it allows the propagation of the information forward in time (Pendergrass et al., 2012; Matsikaris et al., 2015). This has been highlighted in Goosse (2017) where the oceans predominate. It also has the advantage of providing reconstructions that are consistent with changes in forcing as the temporal consistency is kept. However, online methods are computationally very expensive, which limits the ensemble size especially when using complex and high-resolution models. Furthermore, previous studies have shown that off-line methods can be adequate and provide skilful data assimilation-based reconstructions using various kinds of data, for instance surface temperature-related, hydroclimatic-related or even sea surface temperature-related data (e.g., Steiger et al., 2014; Hakim et al., 2016; Klein and Goosse, 2018; Steiger et al., 2018). Moreover, Steiger et al. (2017) recently performed successful off-line data assimilation experiments based on Kalman filtering (Kalnay, 2003) using δ18O in ice-core records. Finally, an off-line data assimilation method (in this study) allows for the use of the results from the isotope-enabled ECHAM5/MPI-OM (Werner et al., 2016) and ECHAM5-wiso (Steiger et al., 2017) models (see Sect. 2.1), which explicitly simulate the δ18O in precipitation, leading to a straightforward and direct comparison in the data assimilation process. This is a clear advantage over inferring the model δ18O based on a linear-univariate fit with local temperature as done, for instance, in Goosse et al. (2012), given the nonlinearity and nonstationarity of the link between stable oxygen ratios and surface temperature (e.g., Masson-Delmotte et al., 2008).
There are two types of off-line data assimilation methods which differ in the way the model ensembles are produced. They can be referred to as transient and stationary off-line methods. In transient methods (e.g., Goosse et al., 2006; Bhend et al., 2012; Matsikaris et al., 2015), an ensemble of simulations is first generated by performing several simulations with one model driven by realistic estimates of the forcing. The ensemble of states used for the data assimilation (i.e., the prior) is time-dependent and changes at every assimilation step, as the model results and the data must correspond to the same time (generally the same year). As for online methods, transient off-line methods have the advantage of providing reconstructions that are consistent with changes in forcings. However, obtaining skillful reconstructions depends on the range of the ensemble, which must be wide enough to capture the full complexity included in the data network. This is directly related to the ensemble size, which is strongly limited in transient off-line methods by the computational constraints on performing ensemble simulations. In stationary off-line methods (e.g., Steiger et al., 2014; Hakim et al., 2016; Steiger et al., 2018), the ensemble of states used for the data assimilation is obtained by selecting not only the time in the simulations corresponding to the data assimilation time step (and thus the observed changes) but also other simulated time steps. This allow for the ensemble size to be increased by several orders of magnitude and thus potentially increases the skill of the reconstructions. However, as the prior includes years with many different forcings, the resulting reconstructions may be inconsistent with changes in the forcing history. This is still valid when internal variability dominates over the forced response, as is the case with hydroclimate-related variables at local scale for instance (e.g., Klein and Goosse, 2018). If the fingerprint of the forcing is large, the data assimilation procedure can also select for reconstructing a specific year, only simulated years characterized by forcings similar to the target year. However, it is also possible that the forcing contribution is underestimated in the reconstruction due to the selection of the prior, inducing some different teleconnections to the teleconnections observed, challenging the interpretation of the reconstructed patterns.
Here, as only one respective simulation exists for ECHAM5/MPI-OM and ECHAM5-wiso, the ensembles are fixed and produced in both cases by selecting all simulated years of these single simulations; this results in ensembles containing 1200 members for ECHAM5/MPI-OM and 141 members for ECHAM5-wiso. The particle filter used (Dubinkina et al., 2011) is implemented in the same way as in Klein and Goosse (2018); it is also detailed in their paper, so only a short description follows. For each assimilation time step (yearly, see Sect. 2.4), every member of the ensemble of simulated climate states is compared to data. The model–data comparison is performed using anomalies over the whole period covered by the simulations in order to remove any potential model biases and to focus on the variability. Based on this comparison, the likelihood, a measure of the ability of the different members to reproduce the signal recorded in the data, is computed the uncertainties of the data taking into account. A weight proportional to the likelihood is then attributed to each member, which allows for the computation of the weighted mean for each assimilation time step and provides the reconstruction.
2.4 Experimental design for data assimilation experiments
The potential for reconstructing the Antarctic surface temperature based on the assimilation of the seven subregional composites of δ18O is first assessed in a controlled framework using pseudoproxy experiments. In this case, pseudoproxies are generated to match the real data of Stenni et al. (2017) as closely as possible, described in Sect. 2.2. First, ECHAM5/MPI-OM δ18O results over the grid cells containing real ice-core records are extracted. As some records fall within a same grid cell, the total number of independent series is reduced from 112 to 52. The precipitation-weighted annual means of δ18O are then computed from these time series, over which a Gaussian white noise is added in order to end up with SNRs of 0.5. This value is commonly used to produce pseudoproxies (Smerdon, 2012), although it reaches the upper range of an average annual mean proxy (Wang et al., 2014). However, as the noise is applied directly to the measured quantity (δ18O) and not to the climatic interpretation inferred from proxy (temperature), it seems adequate. To match the real data temporal resolution, the time series are 10- and 5-year averaged over the 800–1800 and 1800–2000 CE periods, respectively. The 52 time series are then assigned to one of the seven regions and a weight, proportional to the observed surface temperature relationship of the individual record with the corresponding region, is attributed to each pseudoproxy, in the same way as in Stenni et al. (2017). A weighted average by subregion is then performed to produce the seven pseudoproxy composites. Lastly, a temporal mask is applied to the seven time series to match the same time coverage as the reconstructions of Stenni et al. (2017).
The most natural choice would be to apply the same 10- and 5-year averaging procedure to the model results. However, this drastically reduces the ensemble size and thus the range of possible climate states, limiting the data assimilation-based reconstructions skill. Hence, the pseudoproxies are linearly interpolated at the annual resolution which allows for the assimilation frequency to be set to annual and thus uses all available individual years in the two models to build the ensembles, as mentioned in the previous section. The assimilation process is carried out separately for the two model ensembles. The ensembles consist of the seven subregional time series for each year of the simulations, produced by averaging the precipitation-weighted annually averaged results in every grid cell of each region. Note that in the case of the assimilation of pseudoproxies derived from ECHAM5/MPI-OM using the ECHAM5/MPI-OM model ensemble, the model result corresponding to the same year as the assimilated pseudoproxy is excluded from the ensemble at each data assimilation step.
Data assimilation requires an estimate of observation uncertainties. In the case of the pseudoproxy experiments, the uncertainty of the seven time series corresponds to the variance of the noise added in the generation of those data, ranging from 0.15 ‰ for the East Antarctic plateau to 0.47 ‰ for the Weddell Sea coast. Unfortunately, it is not possible to accurately determine the uncertainty associated with real data. Several experiments have been performed using different estimates of observational errors to assess the sensitivity of our results to this parameter. For instance, the error has been assumed to be spatially coherent (using values of 0.15 ‰, 0.25 ‰ or 0.50 ‰), estimated as being proportional to the data series variances, inversely proportional to the number of individual data series contained in a same model grid cell, or a combination of the above. These different estimates of the data uncertainty have an impact on the results, but, as shown in the Sect. S2 in the Supplement, this impact is limited in our experiments. Consequently, a temporally and spatially constant estimate for the data uncertainty equal to 0.25 ‰ is preferred over more complex choices that may be hard to justify given the subjective considerations implied.
2.5 Statistical reconstruction methods
In Sects. 4.2 and 5, the data assimilation-based temperature reconstructions are compared to the statistical reconstructions presented in Stenni et al. (2017), including the previous Antarctica2k temperature reconstruction published by PAGES 2k Consortium (2013) based on the CPS approach. Each of these reconstruction methods is applied to the same input data, whether it be the pseudoproxy or the real data consisting of the ice-core records collection of Stenni et al. (2017).
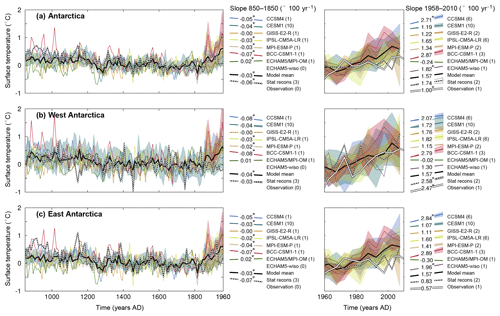
Figure 1Changes in 10- (left panels) and 5-year averaged (right panels) surface temperature over the 850–2000 CE period over (a) Antarctica, (b) West Antarctica and (c) East Antarctica (for a definition of the regions see Stenni et al., 2017). The model results are shown using the colored lines, the average of the three statistical reconstructions of Stenni et al. (2017) is shown using a dashed black and white line, and the reconstruction based on instrumental records (Nicolas and Bromwich, 2014) is shown using a white line (in the right panels only). The number of ensemble members for each model is given in brackets after the labels. The colored shading represents the mean ±1 standard deviation of the corresponding ensemble. The reference period is 1500–1800 CE for the left panels, and 1960-1990 CE for the right panels. The mean slopes (in degree/100 years) over the 850–1850 and 1958–2010 CE periods are shown to the right of each panel; slopes proportional to the numbers are also displayed. When the trends of all available members are significantly different from zero according to F tests (p<0.05), the mean slope values are followed by an asterisk (*).
The reconstruction methods developed in Stenni et al. (2017) are based on linear regressions of ice-core δ18O with local surface temperature on the regional average products. In the first method, the regional isotope composites were scaled based on the annual δ18O–temperature slopes inferred from a ECHAM5-wiso simulation nudged with ERA-Interim atmospheric reanalyses data (Goursaud et al., 2018), over the 1979–2013 CE period. Given the limited length of the simulation, Stenni et al. (2017) considered annual mean anomalies to compute the slopes and applied these slopes to the 5- and 10-year binned composites. In the second approach, the normalized records were scaled to the instrumental period temperature variance at the regional scale, computed over the 1960–1990 CE period for the 5-year-binned averages and the 1960–2010 CE period for the 10-year-binned averages. Here, in the pseudoproxy framework, the scaling is based on the pseudoproxy of temperature only over the 1950–2000 CE period for both averages.
A similar scaling is used in the CPS method to that utilized in the PAGES 2k Consortium (2013) and applied to the larger Antarctic ice-core database in Stenni et al. (2017). The CPS regional reconstructions consist of weighted averages of the normalized records falling in the subregions: the weights are based on the correlation between the records and the corresponding regional temperature time series over the 1961–1991 CE period. The composites are then scaled to the mean and the variance of the observations over the same period. Compared with the two previous statistical approaches, the CPS method has the limitation of discarding more than half of the records (62 out of 112), because it is limited to the sites where there is an overlap between the δ18O records and direct temperature observations.
Each of these reconstructions rely on the assumption that the instrumental period is representative of longer-term climate variability, which is not the case in data assimilation. These reconstructions are hereafter referred to in this paper as the “statistical reconstructions”.
At the continental scale, PMIP/CMIP models show a long-term cooling in Antarctica between the beginning of the last millennium and 1850 CE (Fig. 1), which is consistent with the results of previous model-based (Goosse et al., 2012; PAGES 2k-PMIP3 group, 2015) and observation-based (Goosse et al., 2012; PAGES 2k Consortium, 2013; Stenni et al., 2017) studies. The decrease in temperature in the reconstructions of Stenni et al. (2017) between 850 and 1850 CE reaches −0.62 ∘C (based on the linear trend, significantly different from zero, p<0.05, according to a F test) on average over the three proposed reconstructions, which is in the range of the PMIP/CMIP models where the simulated cooling lies between −0.01 ∘C (not statistically significant) for GISS-E2-R and −0.72 ∘C (significant) for BCC-CSM1-1. ECHAM5/MPI-OM is the only model that does not simulate this last millennium cooling but rather a weak, although statistically significant, warming over the period.
The last millennium cooling trend is followed from the mid-nineteenth century by a relatively strong warming trend until present-day (Fig. 1). As discussed in Abram et al. (2016), climate models systematically simulate the onset of an anthropogenic warming in the mid-nineteenth century, which is consistent with paleoclimate records in the Northern Hemisphere but not in the Southern Hemisphere where the warming is delayed. This model–data mismatch is observed in Antarctica using the reconstructions of Stenni et al. (2017), especially in the western part of the continent where the delay in the reconstructions compared to models reaches about 100 years (Fig. 1b). For the recent period, when instrumental observations are available (1958–2012 CE), PMIP/CMIP models and the reconstructions slightly overestimate the observed warming: an increase in temperature of 0.82 ∘C for the model mean, an increase of 0.90 ∘C for the mean of the reconstructions based on ice-core records, and an increase of 0.52 ∘C for instrumental observations (Fig. 1). Note, however, that the majority of the trends over this period are not statistically significant at the 0.05 level, given that the short period and the temporal resolution of the 5-year mean strongly limit the number of degrees of freedom. In contrast to other models and observations, ECHAM5/MPI-OM shows a weak, nonsignificant cooling trend over the past 50 years.
Much of the recent warming over Antarctica in the reconstruction based on instrumental observations is due to the strong increase in temperature in West Antarctica, while the East has only weakly warmed over the last 50 years. This east–west difference is also present in the statistical reconstructions, but not in the model mean, which shows a uniform warming over both regions due to anthropogenic forcing (Fig. 2a). The model mean can be seen as the forced response, as the natural variability is removed due to the fact that the ensemble size is large enough. Consequently, based on a similar diagnostic, Smith and Polvani (2017) attributed the spatial pattern to natural variability, using the model simulations from 40 CMIP5 models. The large spread between the models and particularly between ensemble members of the same model confirm the role of natural variability in driving the recent temperature trend. For instance, one of the CESM1 simulations shows a significant increase in temperature of more than 2 ∘C in West Antarctica over the 1958–2005 CE period, while another shows a cooling trend, although nonsignificant, for the same period. As a consequence, some individual runs of CESM1, and also of IPSL-CM5A-LR and GISS-E2-R, simulate a differential warming in Antarctica that resembles the observed warming, with a larger temperature increase in West Antarctica than in East Antarctica; this shows that apparent model–data differences for the recent warming pattern in Antarctica do not imply a fundamental inconsistency between models and data. However, despite these important variations within the individual simulations, most of the runs still simulate an overly homogeneous response over Antarctica compared with instrumental observations.
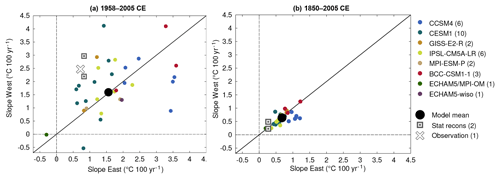
Figure 2Comparison between the reconstructed, simulated and observed surface temperature slopes (in ∘C/100 year) in West Antarctica (y axis) and in East Antarctica (x axis), over the (a) 1958–2005 CE and (b) 1850–2005 CE periods.
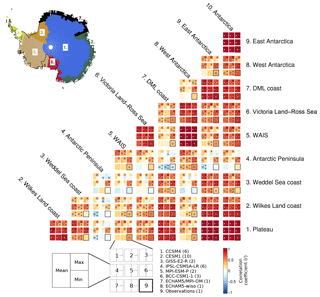
Figure 3Simulated and observed Pearson correlation coefficients between mean annual surface temperature over the 1958–2005 CE period in 10 different subregions covering Antarctica (East Antarctic plateau – referred to as “Plateau”, Wilkes Land coast, Weddell Sea coast, Antarctic Peninsula, WAIS, Victoria Land–Ross Sea, DML coast, West Antarctica, East Antarctica and Antarctica as a whole). The order displayed for the models and the observation values is shown below the main panel. The number of ensemble members for each model is indicated in parentheses. For each model, the mean of the correlations over all the members is shown, along with the value of the ensemble member that has the highest (max) and the lowest (min) correlation. The presence of a white circle represents combinations for which the null hypothesis of no correlation can be rejected at the 0.05 level. In the case of the mean value, there is the white circle if the majority of the ensemble members are statistically significant. The observation is the reconstruction based on the instrumental observations of Nicolas and Bromwich (2014).
It is worth noting that the values of the slopes are sensitive to the interval chosen. Shifting the period by 5 years forward and backward can lead to a difference, although the conclusions drawn from the values of the slopes hold (not shown). In contrast, this behavior changes when the longer period from 1850 to 2005 CE is taken into account (Fig. 2b). In this case, which is consistent with one of the two statistical reconstructions, almost all individual realizations of the models are situated on the diagonal line representing equal trends in eastern and western Antarctica, with a much reduced spread. However, with the exception of ECHAM5/MPI-OM, all models overestimate the warming in both regions compared with the statistical reconstructions. Unfortunately, the period covered by the instrumental record is too short to confirm or reject this uniform warming.
The next step involves investigating whether the uniform response shown by the majority of the models during the observation period (1958–2005 CE) is related to a general overestimation of the correlations between the Antarctic regions compared with the reconstructions based on instrumental data. In order to have a more comprehensive analysis of the link between Antarctic regions, the seven subregions defined in Stenni et al. (2017) are considered here in addition to the wider eastern and western Antarctica domains. In the reconstruction based on instrumental data, the link between annual mean surface temperature over East Antarctica and West Antarctica is relatively weak – although statistically significant – with a correlation coefficient reaching 0.39 (Fig. 3). This is consistent with the difference observed in trends. The lack of a strong relationship is mainly due to the Antarctic Peninsula, incorporated in West Antarctica, which appears isolated from the rest of Antarctica. This is also the case, although to a lesser extent, for the Weddell Sea coast, which is included in East Antarctica.
The simulated link between eastern and western Antarctica is rather consistent for each model and similar to the observed link, as deduced from the mean of the correlation coefficients computed for each ensemble member. There is one exception with respect to the BCC-CSM1-1 model that clearly overestimates the correlation, partly due to a very strong and homogeneous warming over the Antarctic, with BCC-CSM1-1 simulating the highest increase in temperature over the last 50 years. CCSM4 and CESM1, which contain 6 and 10 ensemble members, respectively, show a relatively wide range among members that contain the observed values, with correlation coefficients between both regions varying from 0.30 to 0.65 and from 0.11 to 0.69, respectively. In contrast, all six individual members of IPSL-CM5A-LR simulate quite similar relationships between temperature over eastern and western Antarctica, ranging from 0.45 to 0.62.
The correlations between the other subregions are generally of the same magnitude in the models and the observations. Only one clear bias is observed in the link between the Weddel Sea coast and Antarctica as a whole, with the relationship being overestimated by all of the individual simulations of the climate models. This is related to a simulated warming in this region, whereas the reconstruction based on instrumental observations shows no clear trend. Out of the eight models used, only BCC-CSM1-1 and ECHAM5/MPI-OM are systematically biased, with an overly homogeneous or overly heterogeneous surface temperature over Antarctica, which is partly related to their overestimated and underestimated recent warming, respectively.
Therefore, there are generally no clear and systematic biases in the magnitude of the simulated correlations between subregions of Antarctica. Some models show differences with data, but there is no common rule towards an overestimated or underestimated link; however, virtually all individual model representations show a more homogeneous trend in eastern and western Antarctica compared to data over the 1958–2005 CE instrumental period (Fig. 2a). Obviously, there is a link between correlations between subregions and the similarity of the simulated trends. For instance, the highest (lowest) correlation coefficients between East Antarctica and West Antarctica simulated by BCC-CSM1-1 (ECHAM5/MPI-OM) coincide with the highest (lowest) trend values. Moreover, the wide range of trends simulated by the ensemble members of CESM1 results in a wide range of correlations between the two regions. However, this behavior is not straightforward and is highly model-dependent, rejecting the idea that the spatial coherency of the simulated trends over Antarctica can be explained by the common interannual variability of temperature among Antarctic regions alone.
4.1 Relationship between δ18O and surface temperature in models over the last millennium
The potential for reconstructing surface temperature based on water stable isotopes is first assessed by examining the correlation coefficients and the slopes between δ18O and surface temperature variations over the periods covered by the isotope-enabled models used. In order to resemble the temporal resolution of the data while also having a statistically significant analysis, the relationship between δ18O and temperature is studied using 5 year bins. At the continental scale, the correlation coefficient between δ18O and surface temperature simulated by ECHAM5/MPI-OM reaches 0.57 and the slope is 0.78 ∘C ‰−1 over the 800–1999 CE period (Fig. 4, no. 10). The δ18O–surface temperature relationship is not spatially homogeneous. The Antarctic Peninsula and the Victoria Land–Ross Sea sectors are characterized by particularly low correlation coefficients, with values of 0.43 and 0.45, respectively. In contrast, the East Antarctic plateau shows the strongest relationship with the correlation between both variables reaching 0.66. The mean slopes over the last millennium are more uniform among regions with values ranging between about 0.7 and 0.9 ∘C ‰−1, with the exception of the Victoria Land–Ross Sea region where the slope drops to 0.43 ∘C ‰−1.
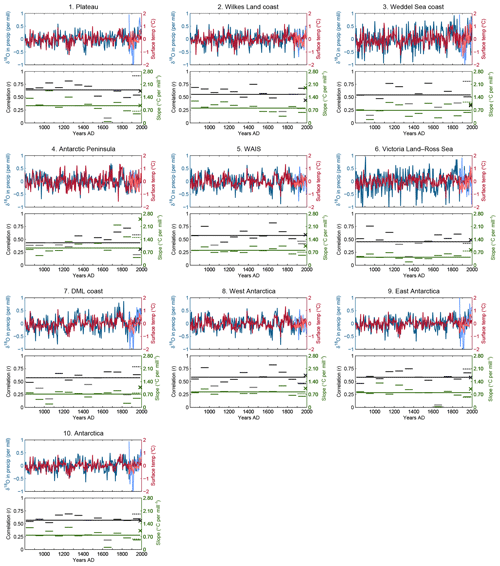
Figure 4Upper panels: evolution of 5-year averaged δ18O in precipitation (blue) and surface temperature (red) over the 800–1999 CE period in ECHAM5/MPI-OM and over the 1871–2011 CE period in ECHAM5-wiso (lighter colors). Lower panels: Pearson correlation coefficients (black) and slope (in ∘C ‰−1, in green) between the two variables in ECHAM5/MPI-OM (horizontal solid bars) and in ECHAM5-wiso (horizontal dashed bars). The lengths of the bars correspond to the period over which the diagnostics are computed. The black bars filled with white represent that the correlation is not statistically significant at the 0.05 level. The diagnostics were only computed over the 1900–2000 CE period for ECHAM5-wiso. The crosses represent the correlation coefficients and the slopes (in ∘C ‰−1) between the same variables based on another ECHAM5-wiso simulation, over the 1979–2013 CE period, using annual mean values (Stenni et al., 2017).
The δ18O–temperature link varies greatly through time as can be seen when considering 100-year intervals (Fig. 4). At the continental scale, there is a strong decline of the δ18O–temperature link between 1600 and 1700 CE, where the correlation coefficient drops to 0.18 (not significant at the 0.05 level). The other centuries of the millennium are characterized by correlation coefficients varying from 0.52 to 0.69 for the 1000–1100 CE and 1200–1300 CE periods, respectively. A similar variability is observed for the slopes, with values between 0.12 ∘C ‰−1 in 1600–1700 CE and 1.21 ∘C ‰−1 in 1200–1300 CE. This variability in the diagnostics does not seem to be linked to the mean climate in a systematic way, but rather appears to be random.
The temporal variability in the correlations and the slopes is even higher at the regional scale. For Antarctica, each subregion has experienced both centuries with nonsignificant relationships and centuries characterized by a strong δ18O–temperature link over the past millennium. The relative temporal variation of the slopes and the correlation coefficients over the last millennium strongly differ among regions, suggesting no clear imprint of the forcings on the δ18O–temperature link. Sime et al. (2008) showed that the δ18O–temperature relationship is reduced when the climate is warmer on Antarctica, based on CO2 increase simulations using the isotope-enabled version of the HadAM3 model. This is not observed in the results in this study, which showed a last century in the range of what is simulated over the past millennium by ECHAM5/MPI-OM, but this was expected given the very limited recent warming shown by the model (Fig. 1).
Over the twentieth century, the simulated δ18O–temperature links of ECHAM5/MPI-OM and ECHAM5-wiso are of the same order of magnitude at the continental scale, with correlation coefficients of 0.69 vs. 0.60 and slopes of 0.57 ∘C ‰−1 vs. 0.52 ∘C ‰−1, respectively. However, the δ18O–temperature link becomes strongly different at the regional scale, with generally higher correlation coefficients and slopes simulated by ECHAM5-wiso. These values cannot be directly compared to those obtained using another simulation of ECHAM5-wiso nudged with ERA-Interim atmospheric reanalyses data from 1979–2013 CE (Goursaud et al., 2018), which was utilized in Stenni et al. (2017), given the different time coverage and resolution (1-year mean instead of 5-year mean). However, it is striking that the slopes are systematically higher in the latter simulation. This is especially notable in the Wilkes Land coast and Antarctic Peninsula regions, where the slopes reach 1.91 and 2.50 ∘C ‰−1, respectively, in the ECHAM5-wiso simulation used in Stenni et al. (2017), compared with corresponding values of 0.57 and 0.41 ∘C ‰−1 for ECHAM5/MPI-OM and 0.78 and 1.51 ∘C ‰−1 for the ECHAM5-wiso of Steiger et al. (2017). This clearly shows the sensitivity of the δ18O–temperature relationship.
It is not possible to provide the precise reason explaining the differences observed between models. One element that may contribute is the time resolution over which the slopes and the correlation coefficients are computed. Indeed, the relationship between δ18O and surface temperature is dependent – although weakly – on the smoothing applied to the time series. Considering 1- or 10-year averages instead of the 5-year averages used here provides slightly different results (Fig. S2). These differences are minimal at the continental scale, but this masks variations between regions. Some regions, such the Victoria Land–Ross Sea area, show a decrease of the correlation coefficient and the slope if the bin size over which the averages are performed increases, whereas others, such as the DML coast area, show the opposite. However, the differences in the δ18O–temperature between 1-, 5- and 10-year averages are generally small. Besides the fact that the diagnostics could not be computed exactly the same way due to model simulation coverage, the differences in model resolution, as well as the influence of natural variability, may play a role in the differences observed between the simulated δ18O–temperature link
These results show that the well-known covariance between δ18O and surface temperature is relatively weak, and that it changes over time in ECHAM5/MPI-OM with no apparent link to forcings. Furthermore, it is model simulation-dependent and to some extent smoothing-dependent, but not in a systematic way. If this is a real characteristic applicable to Antarctic isotopes, then this can limit the skill of temperature reconstructions based on statistical methods that rely on a calibration period which may be too short to be representative. Thus, it is instructive to test a data assimilation method which has the potential advantage of being able to take the temporal changes in the link between temperature and stable isotopes into account and thus reduce the uncertainties.
4.2 Pseudoproxy experiments
This section deals with the potential for reconstructing surface temperature from water stable isotopes, based on pseudoproxy experiments. Using such a controlled framework allows us to precisely assess the performance of the different reconstruction methods via a series of diagnostics including the root mean square error (RMSE) and the correlation coefficients between the reconstructions and the model target (model simulations from which the pseudoproxies are derived), the coefficient of efficiency (CE) of the reconstructions, and the standard deviation of the model truth and the reconstructions. The CE (Lorenz, 1956), which is classically used to measure the skill of reconstructions (e.g., Steiger et al., 2014; Klein and Goosse, 2018), is defined for a time series including n samples as follows:
where x is the “true” time series, is the “true” time series mean, and is the reconstructed time series, i.e., the output after data assimilation or after the statistical reconstruction. The CE ranges from 1, corresponding to a perfect fit between the “true” and the reconstructed time series, to −∞. It is negative when the mean of the “true” time series is a better estimate than the reconstructed time series, meaning that the latter has no skill.
The input data for the reconstructions are δ18O pseudoproxies derived from the ECHAM5/MPI-OM simulation as explained in Sect. 2.4. Statistical reconstruction methods require the use of the individual δ18O pseudoproxies (averaged over a grid) as input, whereas the related seven Antarctic subregions composites are used as input in the data assimilation experiments (see Sect. 2.4 for more information). It is also possible to directly assimilate the individual δ18O pseudoproxies. This gives relatively similar reconstructions, although slightly less skilful in our tests. As a consequence, only the results with the assimilation of the seven composites are shown here.
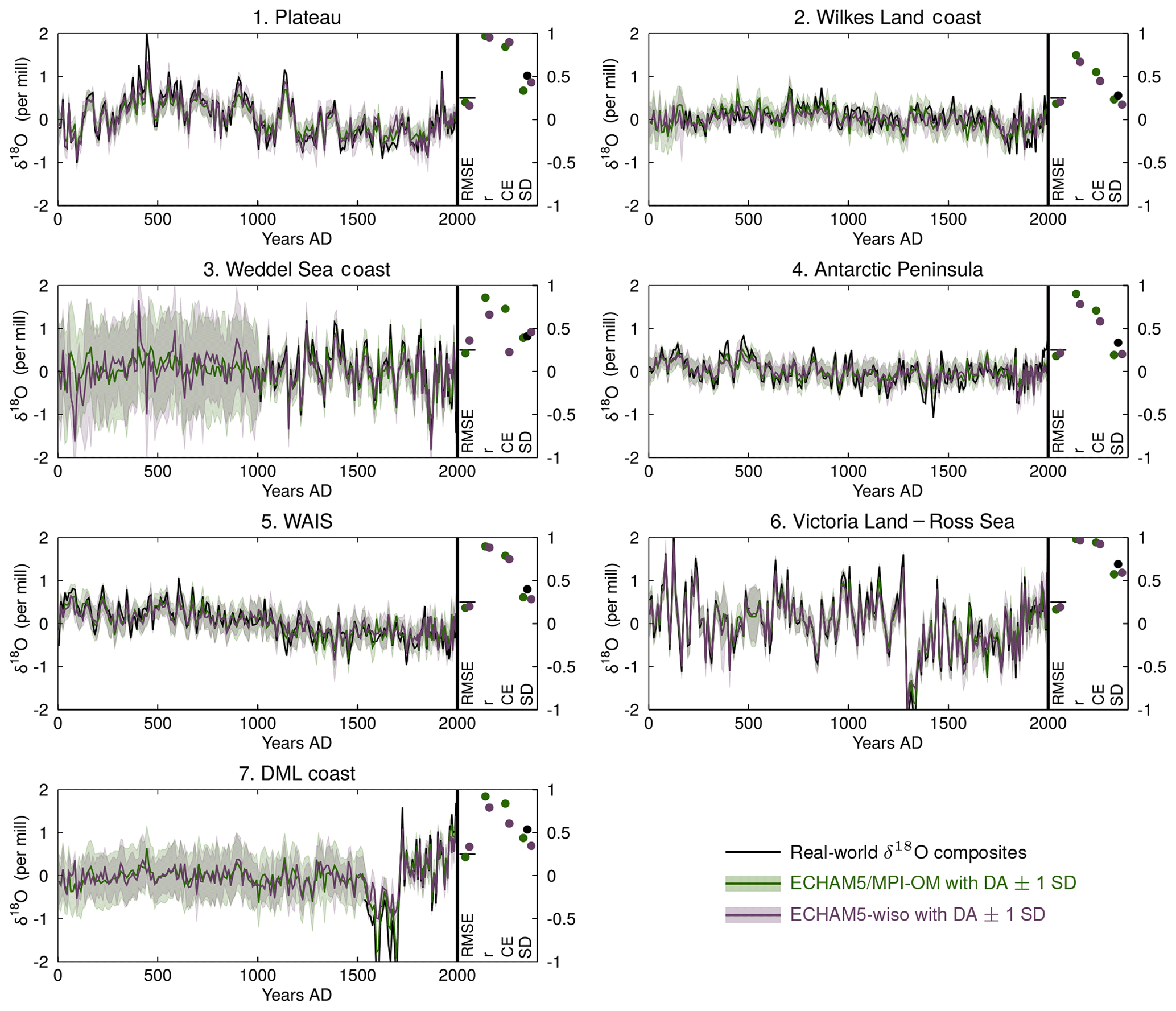
Figure 5Changes in δ18O in precipitation over the 800–2000 CE period in the model truth (ECHAM5/MPI-OM, from which the assimilated pseudoproxies are derived, in black), and in the data assimilation-based reconstructions using the ECHAM5/MPI-OM (in green) and ECHAM5-wiso (in violet) model ensembles. The results are 10-year averaged over the 800–1800 CE period and 5-year averaged over the 1800–2000 CE period. All series are anomalies using the whole periods as a reference. The uncertainty of the reconstructions is shown using colored shading (±1 standard deviation of the model particles scaled by their weight around the mean). Diagnostics related to the skill of the reconstructions are displayed on the right of each panel: the RMSE between the reconstructions and the model target (rmse, in per mill) along with the pseudoproxy error estimates (the horizontal black lines), the correlation coefficients between the reconstructions and the model target (r), the coefficient of efficiency of the reconstructions (ce), and the standard deviation of the reconstructions and the model target (SD).
4.2.1 Data assimilation of δ18O
The assimilation of a δ18O pseudoproxy derived from ECHAM5/MPI-OM allows one (as expected) to provide reconstructions that are very close to the targets, i.e., the ECHAM5/MPI-OM series without any noise added, both when using ECHAM5/MPI-OM and when using ECHAM5-wiso ensembles (Fig. 5). The RMSE with the model truth reach values slightly lower than the errors of the pseudoproxies, which is the best result that can be achieved assuming no spatial propagation. The correlation coefficients and the coefficients of efficiency of the reconstructions exceed 0.90 and 0.70 in all regions, except in the Wilkes Land coast and the Antarctic Peninsula, where a slight decrease in the reconstruction skill is observed in the experiment using the model ensemble derived from ECHAM5-wiso. Thus, overall, ECHAM5-wiso can reproduce the temporal and spatial pattern of δ18O in Antarctica for the δ18O pseudoproxies derived from ECHAM5/MPI-OM. Despite the very different behaviors regarding temperature trends over the last century shown by the two models (Sect. 3), there are no fundamental inconsistencies between them. However, reconstructing δ18O based on the assimilation of δ18O is only the minimum requirement for skilful reconstructions of temperature.
4.2.2 Reconstruction of temperature
Considering Antarctica as a whole, the different methods for reconstructing temperature based on δ18O pseudoproxies perform similarly, with correlations with the model truth ranging from 0.52 for the data assimilation-based reconstruction using the ECHAM5-wiso ensemble to 0.64 for the data assimilation-based reconstruction using the ECHAM5/MPI-OM ensemble (Fig. 6, all coefficients significant at the 0.05 level). Thus, there is some potential for reconstructing the Antarctic temperature based on δ18O data. However, the temperature reconstruction skill is limited, and is much lower than for the reconstruction of δ18O (Fig. 5), which once again demonstrates the weak relationship between δ18O and temperature (Sect. 4.1).
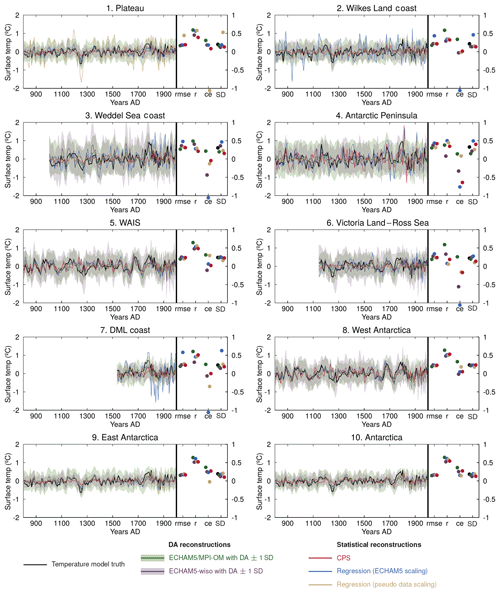
Figure 6Changes in surface temperature over the 800–2000 CE period in the model truth (ECHAM5/MPI-OM, from which the δ18O assimilated pseudoproxies are derived, in black), and in the different data assimilation (in green and violet, see Sect. 2.3) and statistical (in red, blue and beige, see Sect. 2.5) reconstructions based on the δ18O pseudoproxies (Fig. 5). The uncertainty of the data assimilation-based reconstructions is shown using colored shading (±1 standard deviation of the model particles scaled by their weight around the mean). The results are 10-year averaged over the 800–1800 CE period and 5-year averaged over the 1800–2000 CE period. All series are anomalies using the whole periods as a reference. Diagnostics related to the skill of the reconstructions are displayed on the right of each panel: the RMSE between the reconstructions and the model target (rmse, ∘C), the correlation coefficients between the reconstructions and the model target (r), the coefficient of efficiency of the reconstructions (ce), and the standard deviation of the reconstructions and the model target (SD). Coefficient of efficiency values that are lower than −1 are displayed just above the label “ce”.
At the subregional scale, the reconstruction skill generally decreases, and large differences between the reconstruction methods arise. In this case, there is no discernible best reconstruction method, apart from data assimilation using the ECHAM5/MPI-OM ensemble that provides the most skilful reconstructions in all regions. This was expected as the δ18O pseudoproxies used as input for the temperature reconstructions are derived from ECHAM5/MPI-OM, meaning that, in this case, the model physics should be perfect. These reconstructions using the ECHAM5/MPI-OM ensemble are skilful in most individual regions with correlations with the temperature model truth ranging from 0.37 in the Antarctic Peninsula to 0.65 in the WAIS, and positive coefficients of efficiency (Fig. 6). Using the same model for producing both the pseudoproxies and the ensemble of climate states used in the data assimilation process is a strong simplification of reality, which likely artificially inflates the skill of the data assimilation approach (e.g., Smerdon et al., 2016; Klein and Goosse, 2018). Introducing biases in the model physics by selecting model states from ECHAM5-wiso to reconstruct temperature indeed shows decreased skill, with correlation coefficients with the model truth ranging from 0.08 (not significant at the 0.05 level) in the Antarctic Peninsula to 0.48 in the WAIS. The decrease in skill in this case is particularly visible when using coefficients of efficiency, with five regions out of seven characterized by negative coefficients. This is not related to a problem in the variance but rather to issues in representing the relative changes. Indeed, the standard deviation of the series is relatively similar in both data assimilation-based reconstructions for each region, and is slightly underestimated compared to the model truth.
The data assimilation reconstructions using the ECHAM5-wiso ensemble are not systematically closer to the model truth than the statistical reconstructions. They are even outperformed in terms of correlation in the Antarctic Peninsula, and, to a lesser extent, in the DML coast region, which may be related to inconsistencies in the model physics and in the spatial structures compared with the pseudoproxy. More generally, no reconstruction method tends to systematically outperform the others except for data assimilation using the ECHAM5/MPI-OM model ensemble. Large discrepancies between the methods' skill are observed in all subregions. They are mainly due to differences in the magnitude of the temperature changes in statistical reconstructions , rather than to the relative variability, as is the case between both data assimilation-based reconstructions. For instance, on the East Antarctic plateau, while the statistical reconstruction that is scaled based on the variance of the pseudoproxy over the 1950–2000 CE period has the second-highest correlation with the model truth over the last millennium (r=0.57), it has the lowest coefficient of efficiency (CE ) due to a much overestimated variance (standard deviation of the series of 0.53∘ compared with 0.20∘ for the target). This highlights the limits of the assumption of the representativeness of a short calibration period over a longer calibration period. Similar mismatches in variance are observed in the other statistical-based reconstructions. The statistical reconstruction based on the ECHAM5-wiso scaling over the recent past overestimates the standard deviation of the temperature series in the Wilkes Land coast by a factor 2 , in the DML coast by a factor 3, and in the Weddell Sea coast and in the Victoria Land–Ross sea sector by a factor 1.5. As for the previous reconstruction, this can be related to a calibration period not representative of the past, and also to differences in the δ18O–surface temperature link in the simulation used to scale the reconstructions and in the simulation from which the pseudoproxies are derived. The CPS-based reconstructions are in the range of the other reconstruction methods in every subregion with respect to the different diagnostics. As for the data assimilation-based reconstructions, this method can be considered to be relatively robust in this case, as it does not provide any reconstructions with strongly unrealistic variances, unlike the scaling methods.
In the same fashion as for the pseudoproxy experiments, here we first assess whether model results match the δ18O reconstructions of Stenni et al. (2017) in the data assimilation experiments. This is needed to potentially obtain skillful temperature reconstructions. However, given the relatively weak link between δ18O and temperature evidenced in Sect. 4.1 and 4.2, the skill of these temperature reconstructions is expected to be limited even if the data assimilation process technically works well.
5.1 Data assimilation of δ18O
Generally, the data assimilation-based δ18O reconstructions using both the ECHAM5/MPI-OM and ECHAM5-wiso models follow the trends and the variability shown in the seven regional time series of δ18O presented in Stenni et al. (2017) well, as indicated by high correlation coefficients, low RMSE values close to the data uncertainty, and clearly positive coefficients of efficiency (Fig. 7). As the data assimilation method is built in such a manner that the model physics are respected, a good match means that there are no inconsistencies between measured and simulated spatial patterns and trends in δ18O in precipitation. Only the reconstructions over the DML coast and the Weddell Sea coast regions show a lower skill, particularly when the model ensemble is derived from ECHAM5-wiso. This is mainly due to an underestimated variance at the decadal scale, related to a limited ensemble size (only 141 model years available in this simulation). Nevertheless, even in this case, the reconstructions still match the assimilated data reasonably well with significant positive correlations and positive coefficients of efficiency.
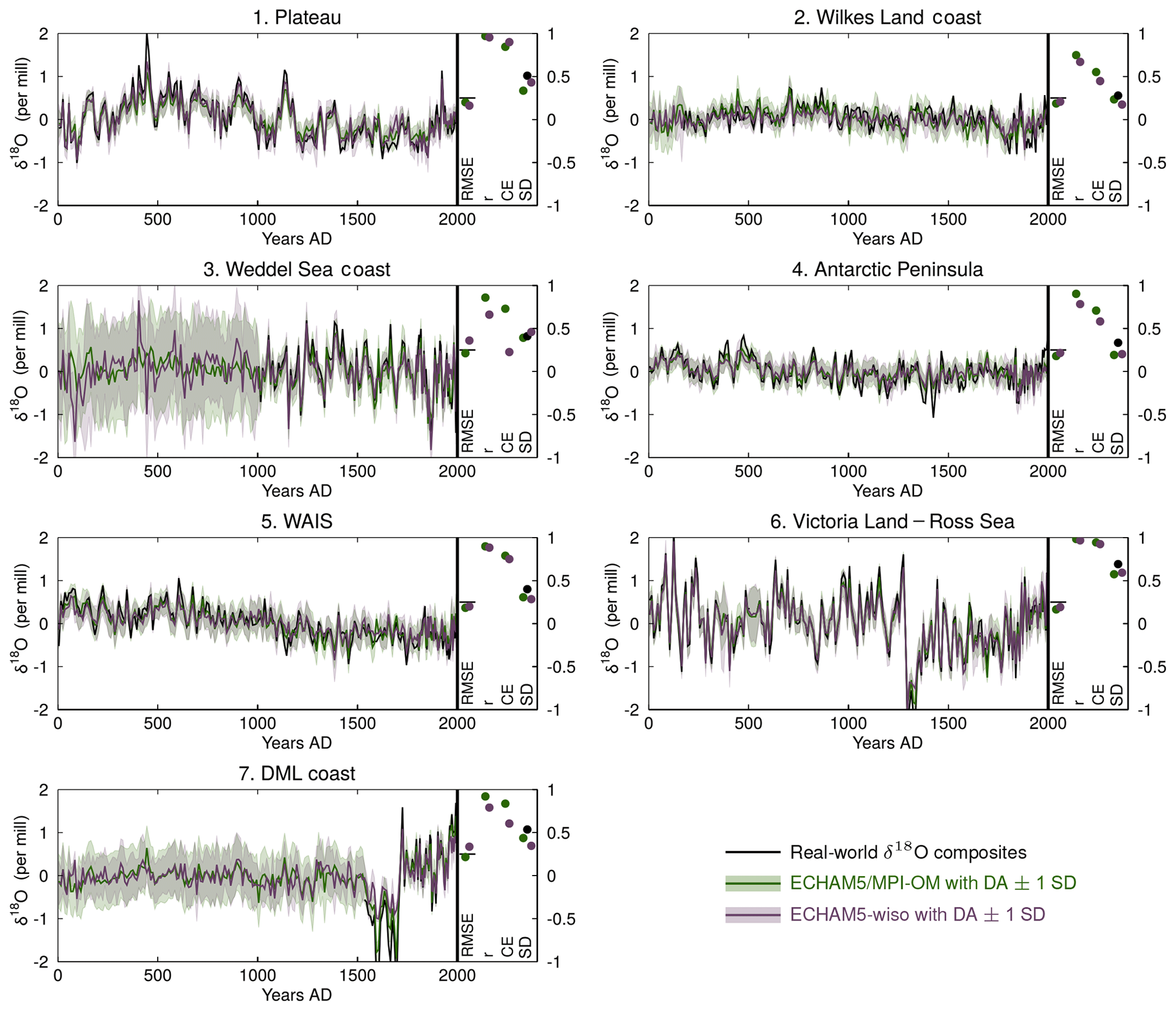
Figure 7Changes in δ18O in precipitation over the 0–2000 CE period in the data assimilated (Stenni et al., 2017, in black), and in the data assimilation-based reconstructions using the ECHAM5/MPI-OM (in green) and ECHAM5-wiso (in violet) models. The results are 10-year averaged over the 800–1800 CE period and 5-year averaged over the 1800–2000 CE period. All series are anomalies using the whole period as a reference. The uncertainty of the reconstructions is shown using colored shading (±1 standard deviation of the model particles scaled by their weight around the mean). Diagnostics related to the skill of the reconstructions are displayed on the right of each panel: the RMSE between the reconstructions and the data assimilated (rmse, in per mill) along with the data error (the horizontal black lines), the correlation coefficients between the reconstructions and the data assimilated (r), the coefficient of efficiency of the reconstructions (CE), and the standard deviation of the data and the reconstructions over the period covered by the data (SD).
From a technical point of view, the data assimilation process works well (see Sect. S3 for technical information). When data are available for assimilation, the uncertainty is reduced meaning that the constraint is strong. When no δ18O data are available, as is the case during the first millennium in the Weddell Sea coast and the first 1500 years in the DML coast, the uncertainty of the data assimilation-based reconstructions, shown as ±1 standard deviation of the model particles with nonzero weight around the mean in Fig. 7, is almost as large as the uncertainty of the original model ensembles (not shown). This indicates a very modest influence of the neighboring regions that have available data on the regions that lack data. This almost total absence of the spatial propagation of the information contained in the assimilated data may be related to weak covariances between some of the regions. This seems to be the case at least for the Weddell Sea coast, which is one of the most isolated Antarctic regions in terms of interannual variability (Fig. 3). This is consistent with the motivation of Stenni et al. (2017) to produce regional-scale reconstructions.
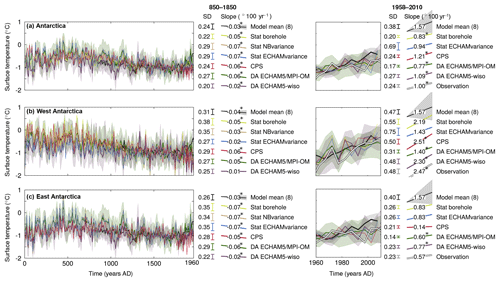
Figure 8Changes in 10- (left panels) and 5-year averaged (right panels) simulated and reconstructed surface temperature over the 0–2000 CE period over (a) Antarctica, (b) West Antarctica and (c) East Antarctica. The model mean and ± one standard deviation of the individual simulations are shown in black and shaded gray, respectively; the statistical reconstructions of Stenni et al. (2017) are shown in yellow, beige and blue. Stat NBvariance uses a temperature scaling based on the temperature observations of Nicolas and Bromwich (2014) over the 1960–2010 CE period (see Sect. 2.5 for more information), Stat ECHAMvariance uses a temperature scaling based on the simulated δ18O–temperature link in a ECHAM5-wiso simulation over the 1979–2013 CE period (Goursaud et al., 2018), and Stat borehole also uses a scaling based on the simulated δ18O–temperature link in ECHAM5-wiso, but the WAIS region is adjusted to match the temperature trend between 1000 and 1600 CE based on borehole temperature measurements from Orsi et al. (2012). The data assimilation reconstructions based on the ECHAM5/MPI-OM and ECHAM5-wiso model ensembles are shown in green and violet, respectively. The uncertainty of the data assimilation-based reconstructions is shown using colored shading (±1 standard deviation of the model particles scaled by their weight around the mean). The reconstructions based on instrumental records (Nicolas and Bromwich, 2014) are shown using a white line (in the right panels only). The reference period is 1500–1800 CE for the left panels, and 1960–1990 CE for the right panels. The standard deviation and the slopes of the series (in ∘C/100 years) are shown for the 850–1850 CE (or overlap period) and 1958–2010 CE periods; slopes proportional to the numbers are also displayed. When the trends are significantly different from zero according to F-tests (p<0.05), the slope values are followed by an asterisk (*).
5.2 Reconstruction of temperature
At the continental scale, both the statistical and data assimilation-based reconstructions show a weak warming during the 0–500 CE period, followed by a long-term cooling trend that ends at about the middle of the nineteenth century (Fig. 8). The cooling over the 850–1850 CE period is of the same order of magnitude in the different reconstructions, with values slightly higher – but still in the range – of the models. Only the reconstruction based on data assimilation using the ECHAM5-wiso ensemble differs from the others, with a weaker – but still statistically significant – cooling over the last millennium, which may be related to the relatively small size of the ensemble and thus the limited range of possible atmospheric states. At this scale, the variance of the different statistical and data assimilation reconstructions is relatively similar over the 850–1850 CE period.
The main discrepancy between reconstructed temperatures and model results without data assimilation is that the onset of the anthropogenic warming is too early, which is especially visible in West Antarctica (Sect. 3). Data assimilation allows for the reconstruction of a later warming, which is consistent with statistical reconstructions. After the mid-nineteenth century, the reconstructed temperature series are characterized by decadal-scale fluctuations with no clear trends, until the mid-twentieth century when the rise in temperature reaches a similar value to that in the reconstruction based on instrumental observations. Over the last 50 years, differences in the variance at the continental scale are observed between the time series, but they are not systematically related to the type of reconstruction method.
Instrumental observations and models without data assimilation also show differences regarding their spatial pattern of the recent trend. The observations clearly display a stronger recent warming in the west than in the east over the past 50 years, while the model mean displays a homogeneous warming over Antarctica (Fig. 8, see Sect. 3 for more details). All reconstructions, including the data assimilation-based reconstructions, match the observed contrast between regions well. However, the difference in trend between both regions is slightly underestimated in the statistical reconstruction based on the ECHAM5 temperature scaling, and in the data assimilation reconstruction using the model ensemble derived from ECHAM5/MPI-OM. The latter case can be explained by the low range of temperature changes covered by the simulated model states for this reconstruction, despite the high number of particles available (Fig. 1). Nevertheless, data assimilation allows the apparent disagreement regarding the recent trends between the ECHAM5/MPI-OM and ECHAM5-wiso models and the observations to be reconciled. We use a stationary off-line data assimilation method. This means that when all of the simulated years are analyzed, the models can simulate a pattern resembling the observed contrasting warming between eastern and western Antarctica. This implies that a pattern such as this is consistent with the model physics and that internal variability likely plays a strong role in the observed pattern, as suggested by the analysis of all of the individual model realizations of the recent trends (Fig. 2a) and of the recent link between the Antarctic subregions (Fig. 4). However, due to our experimental design, there is no guarantee that the contribution of the forcings is well accounted for. For instance, we cannot rule out that, although the pattern is compatible with internal variability, it may be totally masked in some models by an overly strong response to the forcing, leading to an incompatibility with observations.
Thus, at the large scale (when considering West Antarctica, East Antarctica and Antarctica as a whole), there is no strong nor systematic difference in trends, over the last millennium or over the recent past, when using a data assimilation technique compared with the statistical methods applied in Stenni et al. (2017) to reconstruct surface temperatures based on water stable isotopes. Furthermore, the variance of the time series produced by the assorted reconstruction methods are quite similar, although the data assimilation-based reconstructions often show slightly lower values. This behavior becomes different when considering a lower spatial scale – the seven subregions (Fig. 9). In this case, the last millennium trends of the different reconstructions remain relatively similar, although some differences exist, for instance, at the Weddell Sea coast where the data assimilation reconstructions disagree regarding the direction of the slope. Note that at this spatial scale, the differences in the model resolution (3.75∘ latitude × 3.75∘ longitude for ECHAM5/MPI-OM and about 1∘ latitude × 1∘ longitude for ECHAM5-wiso) may play a role in this disagreement. Unlike the trends, there are large differences in the variance of the last millennium reconstructions. These differences are found between the data assimilation and the statistical methods, but also among the statistical methods alone, whereas the two data assimilation-based reconstructions show similar variances in every subregion.
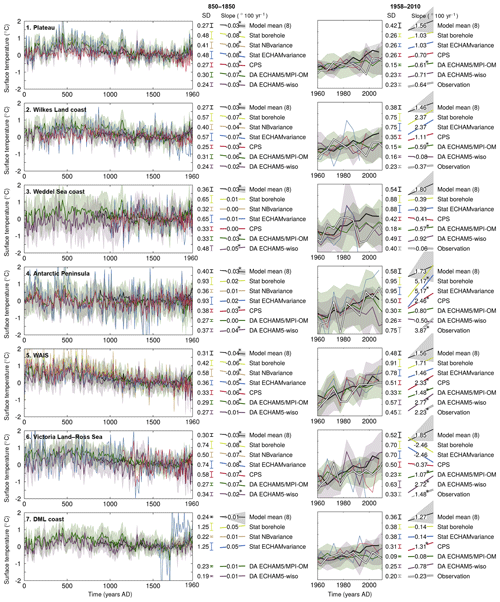
Figure 9Changes in 10- (left panels) and 5-year averaged (right panels) simulated and reconstructed surface temperature over the 0–2000 CE period over the seven Antarctic subregions. The model mean and ± 1 standard deviation of the individual simulations are shown in black and shaded gray, respectively; the statistical reconstructions of Stenni et al. (2017) are shown in yellow, beige and blue. Stat NBvariance uses a temperature scaling based on the temperature observations of Nicolas and Bromwich (2014) over the 1960–2010 CE period (see Sect. 2.5), Stat ECHAMvariance uses a temperature scaling based on the simulated δ18O–temperature link in a ECHAM5-wiso simulation over the 1979–2013 CE period (Goursaud et al., 2018), and Stat borehole also uses a scaling based on the simulated δ18O–temperature link in ECHAM5-wiso, but the WAIS region is adjusted to match the temperature trend between 1000 and 1600 CE based on borehole temperature measurements from Orsi et al. (2012). The data assimilation reconstructions based on the ECHAM5/MPI-OM and ECHAM5-wiso model ensembles are shown in green and violet, respectively. The uncertainty of the data assimilation-based reconstructions is shown using colored shading (±1 standard deviation of the model particles scaled by their weight around the mean). The reconstructions based on instrumental records observations from Nicolas and Bromwich (2014) are shown using white lines (in the right panels only). The reference period is 1500–1800 CE for the left panels, and 1960-1990 CE for the right panels. The standard deviation and the slopes of the series (in degree/100 years) are shown for the 850–1850 CE (or overlap period) and 1958–2010 CE periods; slopes proportional to the numbers are also displayed. When the trends are significantly different from zero according to F tests (p<0.05), the slope values are followed by an asterisk (*).
Regarding the past 50 years covered by instrumental records, the agreement between the different methods is strongly region-dependent. For instance, the East Antarctic plateau is characterized by reconstructions with consistent trends and variances, which show a relatively modest warming and a weak variability. In contrast, in the Victoria Land–Ross Sea sector, the reconstructions based on instrumental observations (Nicolas and Bromwich, 2014) and on data assimilation display a recent warming, whereas the statistical reconstructions show the opposite. There are also differences among similar types of reconstruction methods. For the Weddell Sea coast, for instance, the statistical reconstructions do not agree on the sign of the recent trend. This is also seen with both data assimilation-based reconstructions in the Wilkes Land coast and the Antarctic Peninsula. Again, the difference in the model resolution may play a role in this respect. Depending on the region, very large differences in variances can also be found in the time series produced; nevertheless, neither the statistical-based reconstruction method nor the data assimilation method provide reconstruction where the variance is systematically closer to that of the instrumental record-based reconstruction. However, one should be careful in drawing conclusions from the analysis of the last 50 years of the reconstructions, which correspond to the period covered by the instrumental records. This period is indeed very short, especially as only the 5-year mean results are considered, and the seven Antarctic subregions are characterized by a strong variability, which often challenges the significance of the trends.
Unlike in the large-scale analyses, there are large differences between the reconstruction methods at the subregional scale, mainly in terms of variance, which highlights the uncertainties related to the reconstruction method at this scale. As the data assimilation technique used can take a change in time of the δ18O–surface temperature slope into account, and as this slope does seem to change strongly over time (Fig. 4), there are, in theory, advantages to using data assimilation over statistical reconstructions. However, whether the variance is better represented in one reconstruction or another cannot be verified given the limited length of the instrumental record. Finally, the main advantage of using a data assimilation-based method is that beyond the target variable at the locations where data are available, all variables of the system are reconstructed at all of the locations available in the models used. If the reconstruction is consistent with the assimilated data, as is the case here, this allows for the causes of the reconstructed changes to be studied, although this falls outside the scope of the present study.
The goal of this study is to assess the robustness of Antarctic temperature reconstructions published by Stenni et al. (2017) covering the last 2 millennia using climate model results and data assimilation experiments. The potential for reconstructing surface temperature based on water stable isotopes is first examined by characterizing the simulated relationship between both variables through the last millennium in ECHAM5/MPI-OM. The results show that the well-known covariance between δ18O and surface temperature is relatively weak on average. It is characterized by a strong spatial heterogeneity, and changes over time with no apparent link to forcings. Furthermore, the study of the relationship in other isotope-enabled model simulations from ECHAM5-wiso covering the recent past show that the link differs from one model simulation to another, which may indicate the influence of natural variability in the δ18O–surface temperature link, in addition to the influence of the model resolution. If these simulated characteristics are real and applicable to Antarctic isotopes, this limits the skill of temperature reconstructions based on statistical methods which rely on the hypothesis that the last decades (the observation period) provide a good estimate for longer temperature reconstructions. Thus, using a data assimilation method to reconstruct temperature based on δ18O potentially has advantages over statistical methods, as it does not rely on a constant δ18O–temperature link through time and space.
Pseudoproxy experiments confirm the benefits of using a data assimilation method, but also show the relatively weak link between both variables, leading to a limited potential for reconstructing temperature based on δ18O. No reconstruction method stands out compared with the others in terms of relative variability; however, the statistical methods provide reconstructions with unrealistic variances in some subregions, when the calibration period is too short to provide an adequate estimate of the long-term changes of the δ18O–temperature link. In contrast, data assimilation always provides reconstructions with a variance in agreement with the model truth. In general, the skill in reconstructing surface temperature based on δ18O data is limited, even in an optimistic framework where the model physics are assumed to be perfect (when assimilating the pseudoproxy derived from ECHAM5/MPI-OM into a model ensemble constructed from ECHAM5/MPI-OM). It is, however, higher and more uniform among reconstruction methods when the reconstruction targets are the bigger regions – West Antarctica, East Antarctica, and Antarctica as a whole – rather than the seven individual subregions.
Applying the data assimilation method to the real δ18O regional composites of Stenni et al. (2017) demonstrates that there is no fundamental model–data inconsistency in terms of temporal and spatial δ18O changes as the output of the assimilation processes using ECHAM5/MPI-OM and ECHAM5-wiso model ensembles match the data assimilated over the seven Antarctic subregions. As with the statistical reconstructions, the resulting temperature reconstructions confirm the long-term cooling over Antarctica during the last millennium, and the later onset of anthropogenic warming compared with the simulations without data assimilation, which is especially visible in West Antarctica. Furthermore, data assimilation allows for models and instrumental observations to be reconciled by reconstructing the observed east–west contrast of the recent temperature trends. In instrumental observations, much of the recent warming over Antarctica is indeed due to the strong increase in temperature in West Antarctica, whereas East Antarctica has only weakly warmed over the last 50 years. In contrast, the PMIP/CMIP model mean and the mean of the ensemble members of individual PMIP/CMIP models show a uniform warming over both regions following the anthropogenic forcing. Both reconstructions with data assimilation show the observed contrast, indicating that this pattern can be represented by climate models. Furthermore, the large spread of individual model realizations without data assimilation regarding the spatial pattern of the recent warming suggests that internal variability likely plays a major role in driving this heterogeneous recent warming. The internal variability is found to be especially large in West Antarctica, particularly in the Peninsula. The results of data assimilation experiments and the analysis of individual model simulations show that the apparent model–data differences for the recent warming pattern in Antarctica do not imply a fundamental inconsistency between models and data. Still, most model simulations show an overly homogeneous recent trend compared to data over the continent, but this is not related to an overly strong link between regions, with the models being able to simulate correlation coefficients between regional temperature changes of the same order as the observed ones.
Consistent with the results of pseudoproxy experiments, the temperature reconstructions using the different methods are relatively similar over the three large regions (West Antarctica, East Antarctica and Antarctica as a whole). At this large scale, there is no large and systematic difference in past and recent trends, nor in the magnitude of the variability. This gives credibility to these large-scale temperature reconstructions, but it is important to keep in mind that only the uncertainty related to the reconstruction method is assessed here, and not the potential problems related to the spatial distribution of ice-core records, the accuracy of their age scales, and the noise associated with post-deposition processes. The picture is different for the seven subregions, where the variance of the last millennium reconstructions produced by the different methods are different. Although, in theory, there are advantages to using data assimilation over statistical reconstructions that have been confirmed with the pseudoproxy experiments, the instrumental series are too short to confirm this in a realistic setup.
As a perspective, we would like to stress the importance of moving towards the use of a range of climate sensitive proxy records instead of only considering δ18O, given the limited temperature signal present in oxygen isotopes. Assimilating second-order isotopic parameters such as deuterium excess, along with accumulation rates and δ18O would, for instance, certainly give more insight not just into temperature changes but also into moisture transport characteristics, which would help reconstruct hydroclimate variations. However, it seems extremely challenging today as it would require a proper estimation of the observational error for all proxy records, which is difficult to provide. Furthermore, isotope-enabled model simulations covering the last millennium are still rare, despite growing interest in the modeling community (e.g., Werner et al., 2011, 2016; Roche, 2013); furthermore, the skill of isotope-enabled models is difficult to assess over the last millennium given the limited availability of instrumental records. Future studies dealing with δ18O data assimilation experiments should take advantage of ensembles of simulations instead of individual runs, in order to provide a larger range in the simulated states and improve the data assimilation-based reconstructions skill. More generally, an ensemble of simulations would be useful to any future study involving model–data comparisons of oxygen isotopes over the last millennium, to help distinguish the forced response from natural variability.
The main Antarctic temperature and δ18O reconstructions can be downloaded from https://doi.org/10.5281/zenodo.2579204 (Klein et al., 2016). The PMIP3/CMIP5 model results can be downloaded online from the Program for Climate Model Diagnosis and Intercomparison (PCMDI; http://pcmdi9.llnl.gov, last access: 20 April 2018). Products from the ECHAM5-wiso model simulation from 1871 to 2011 CE (Steiger et al., 2017) can be downloaded from https://doi.org/10.5281/zenodo.1249604 (Steiger, 2018). Results from the ECHAM5/MPI-OM model simulation covering the 800–1999 CE period (Sjolte et al., 2018) are available on request from Jesper Sjolte (jesper.sjolte@geol.lu.se).
The supplement related to this article is available online at: https://doi.org/10.5194/cp-15-661-2019-supplement.
The authors declare that they have no conflict of interest.
This work was supported by the Belgian Research Action through Interdisciplinary Networks (BRAIN-be) from the Belgian Science Policy Office in the framework of the “East Antarctic surface mass balance in the Anthropocene: observations and multiscale modelling (Mass2Ant)” project (contract no. BR/165/A2/Mass2Ant). Hugues Goosse is the research director within the F.R.S.-FNRS. Nathan J. Steiger is supported by the US National Science Foundation award no. OISE-1743738. Raphael Neukom is supported by the Swiss NSF (grant no. PZ00P2_154802).
This paper was edited by Julie Loisel and reviewed by two anonymous referees.
Abram, N. J., McGregor, H. V., Tierney, J. E., Evans, M. N., McKay, N. P., Kaufman, D. S., Thirumalai, K., Martrat, B., Goosse, H., Phipps, S. J., Steig, E. J., Kilbourne, K. H., Saenger, C. P., Zinke, J., Leduc, G., Addison, J. A., Mortyn, P. G., Seidenkrantz, M. S., Sicre, M. A., Selvaraj, K., Filipsson, H. L., Neukom, R., Gergis, J., Curran, M. A., and Von Gunten, L.: Early onset of industrial-era warming across the oceans and continents, Nature, 536, 411–418, https://doi.org/10.1038/nature19082, 2016. a
Bhend, J., Franke, J., Folini, D., Wild, M., and Brönnimann, S.: An ensemble-based approach to climate reconstructions, Clim. Past, 8, 963–976, https://doi.org/10.5194/cp-8-963-2012, 2012. a
Casado, M., Landais, A., Picard, G., Münch, T., Laepple, T., Stenni, B., Dreossi, G., Ekaykin, A., Arnaud, L., Genthon, C., Touzeau, A., Masson-Delmotte, V., and Jouzel, J.: Archival of the water stable isotope signal in East Antarctic ice cores, The Cryosphere Discuss., https://doi.org/10.5194/tc-2016-263, 2016. a
Dansgaard, W.: Stable isotopes in precipitation, Tellus, 16, 436–468, https://doi.org/10.1111/j.2153-3490.1964.tb00181.x, 1964. a
Dee, D. P., Uppala, S. M., Simmons, A. J., Berrisford, P., Poli, P., Kobayashi, S., Andrae, U., Balmaseda, M. A., Balsamo, G., Bauer, P., Bechtold, P., Beljaars, A. C. M., van de Berg, I., Biblot, J., Bormann, N., Delsol, C., Dragani, R., Fuentes, M., Greer, A. J., Haimberger, L., Healy, S. B., Hersbach, H., Holm, E. V., Isaksen, L., Kallberg, P., Kohler, M., Matricardi, M., McNally, A. P., Mong-Sanz, B. M., Morcette, J.-J., Park, B.-K., Peubey, C., de Rosnay, P., Tavolato, C., Thepaut, J. N., and Vitart, F.: The ERA-Interim reanalysis: Configuration and performance of the data assimilation system, Q. J. Roy. Meteorol. Soc., 137, 553–597, https://doi.org/10.1002/qj.828, 2011. a
Dubinkina, S., Goosse, H., Sallaz-Damaz, Y., Crespin, E., and Crucifix, M.: Testing a particle filter to reconstruct climate changes over the past centuries, Int. J. Bifurcat. Chaos, 21, 3611–3618, https://doi.org/10.1142/S0218127411030763, 2011. a
Dufresne, J. L., Foujols, M. a., Denvil, S., Caubel, A., Marti, O., Aumont, O., Balkanski, Y., Bekki, S., Bellenger, H., Benshila, R., Bony, S., Bopp, L., Braconnot, P., Brockmann, P., Cadule, P., Cheruy, F., Codron, F., Cozic, A., Cugnet, D., de Noblet, N., Duvel, J. P., Ethé, C., Fairhead, L., Fichefet, T., Flavoni, S., Friedlingstein, P., Grandpeix, J. Y., Guez, L., Guilyardi, E., Hauglustaine, D., Hourdin, F., Idelkadi, A., Ghattas, J., Joussaume, S., Kageyama, M., Krinner, G., Labetoulle, S., Lahellec, A., Lefebvre, M. P., Lefevre, F., Levy, C., Li, Z. X., Lloyd, J., Lott, F., Madec, G., Mancip, M., Marchand, M., Masson, S., Meurdesoif, Y., Mignot, J., Musat, I., Parouty, S., Polcher, J., Rio, C., Schulz, M., Swingedouw, D., Szopa, S., Talandier, C., Terray, P., Viovy, N., and Vuichard, N.: Climate change projections using the IPSL-CM5 Earth System Model: From CMIP3 to CMIP5, Climate Dynam., 40, 2123–2165, https://doi.org/10.1007/s00382-012-1636-1, 2013. a
Ekaykin, A. A., Kozachek, A. V., Lipenkov, V. Y., and Shibaev, Y. A.: Multiple climate shifts in the Southern Hemisphere over the past three centuries based on central Antarctic snow pits and core studies, Ann. Glaciol., 55, 259–266, https://doi.org/10.3189/2014AoG66A189, 2014. a
Gent, P. R., Danabasoglu, G., Donner, L. J., Holland, M. M., Hunke, E. C., Jayne, S. R., Lawrence, D. M., Neale, R. B., Rasch, P. J., Vertenstein, M., Worley, P. H., Yang, Z.-L., and Zhang, M.: The Community Climate System Model Version 4, J. Climate, 24, 4973–4991, https://doi.org/10.1175/2011JCLI4083.1, 2011. a
Goosse, H.: Reconstructed and simulated temperature asymmetry between continents in both hemispheres over the last centuries, Clim. Dynam., 48, 1483–1501, https://doi.org/10.1007/s00382-016-3154-z, 2017. a
Goosse, H., Renssen, H., Timmermann, A., Bradley, R. S., and Mann, M. E.: Using paleoclimate proxy-data to select optimal realisations in an ensemble of simulations of the climate of the past millennium, Clim. Dynam., 27, 165–184, https://doi.org/10.1007/s00382-006-0128-6, 2006. a
Goosse, H., Braida, M., Crosta, X., Mairesse, A., Masson-Delmotte, V., Mathiot, P., Neukom, R., Oerter, H., Philippon, G., Renssen, H., Stenni, B., van Ommen, T., and Verleyen, E.: Antarctic temperature changes during the last millennium: evaluation of simulations and reconstructions, Quaternary Sci. Rev., 55, 75–90, https://doi.org/10.1016/j.quascirev.2012.09.003, 2012. a, b, c, d, e, f
Goursaud, S., Masson-Delmotte, V., Favier, V., Preunkert, S., Fily, M., Gallée, H., Jourdain, B., Legrand, M., Magand, O., Minster, B., and Werner, M.: A 60-year ice-core record of regional climate from Adélie Land, coastal Antarctica, The Cryosphere, 11, 343–362, https://doi.org/10.5194/tc-11-343-2017, 2017. a
Goursaud, S., Masson-Delmotte, V., Favier, V., Orsi, A., and Werner, M.: Water stable isotope spatio-temporal variability in Antarctica in 1960–2013: observations and simulations from the ECHAM5-wiso atmospheric general circulation model, Clim. Past, 14, 923–946, https://doi.org/10.5194/cp-14-923-2018, 2018. a, b, c, d, e, f
Hakim, G. J., Emile-Geay, J., Steig, E. J., Noone, D., Anderson, D. M., Tardif, R., Steiger, N., and Perkins, W. A.: The Last Millennium Climate Reanalysis Project: Framework and First Results, J. Geophys. Res.-Atmos., 121, 6745–6764, https://doi.org/10.1002/2016JD024751, 2016. a, b, c
IAEA/WMO: Global Network of Isotopes in Precipitation, The GNIP Database, available at: http://www.iaea.org/water, last access: 15 January 2018. a
Jones, J. M., Gille, S. T., Goosse, H., Abram, N. J., Canziani, P. O., Charman, D. J., Clem, K. R., Crosta, X., De Lavergne, C., Eisenman, I., England, M. H., Fogt, R. L., Frankcombe, L. M., Marshall, G. J., Masson-Delmotte, V., Morrison, A. K., Orsi, A. J., Raphael, M. N., Renwick, J. A., Schneider, D. P., Simpkins, G. R., Steig, E. J., Stenni, B., Swingedouw, D., and Vance, T. R.: Assessing recent trends in high-latitude Southern Hemisphere surface climate, Nat. Clim. Change, 6, 917–926, https://doi.org/10.1038/nclimate3103, 2016. a, b, c, d
Jones, T. R., Cuffey, K. M., White, J. W., Steig, E. J., Buizert, C., Markle, B. R., McConnell, J. R., and Sigl, M.: Water isotope diffusion in the WAIS Divide ice core during the Holocene and last glacial, J. Geophys. Res.-Earth, 122, 290–309, https://doi.org/10.1002/2016JF003938, 2017. a
Jouzel, J.: Magnitude of isotope/temperature scaling for interpretation of central Antarctic ice cores, J. Geophys. Res., 108, 4361, https://doi.org/10.1029/2002JD002677, 2003. a
Jouzel, J., Alley, R. B., Cuffey, K. M., Dansgaard, W., Grootes, P., Hoffmann, G., Johnsen, S. J., Koster, R. D., Peel, D., Shuman, C. A., Stievenard, M., Stuiver, M., and White, J.: Validity of the temperature reconstruction from water isotopes in ice cores, J. Geophys. Res.-Oceans, 102, 26471–26487, https://doi.org/10.1029/97JC01283, 1997. a
Kalnay, E.: Atmospheric modeling, data assimilation and predictability, Cambridge Univ. Press, Cambridge, UK, 2003. a
Klein, F. and Goosse, H.: Reconstructing East African rainfall and Indian Ocean sea surface temperatures over the last centuries using data assimilation, Clim. Dynam., 50, 3909–3929, https://doi.org/10.1007/s00382-017-3853-0, 2018. a, b, c, d, e
Klein, F., Goosse, H., Graham, N. E., and Verschuren, D.: Comparison of simulated and reconstructed variations in East African hydroclimate over the last millennium, Clim. Past, 12, 1499–1518, https://doi.org/10.5194/cp-12-1499-2016, 2016. a
Klein, F., Abram, N. J., Curran, M. A. J., Goosse, H., Goursaud, S., Masson-Delmotte, V., Moy, A., Neukom, R., Orsi, A., Jesper, S., Steiger, N., Stenni, B., and Werner, M.: Data assimilation-based surface temperature reconstructions over the last two millennia over Antarctica, Data set, Zenodo, https://doi.org/10.5281/zenodo.2579204, 2019. a
Laepple, T., Münch, T., Casado, M., Hoerhold, M., Landais, A., and Kipfstuhl, S.: On the similarity and apparent cycles of isotopic variations in East Antarctic snow pits, The Cryosphere, 12, 169–187, https://doi.org/10.5194/tc-12-169-2018, 2018. a
Lorenz, E. N.: Empirical orthogonal functions and statistical weather prediction, Tech. rep., Statistical Forecasting Scientific Rep. 1, Department of Meteorology, Massachusetts Institute of Technology, Cambridge, MA, 1956. a
Masson-Delmotte, V., Dreyfus, G., Braconnot, P., Johnsen, S., Jouzel, J., Kageyama, M., Landais, A., Loutre, M.-F., Nouet, J., Parrenin, F., Raynaud, D., Stenni, B., and Tuenter, E.: Past temperature reconstructions from deep ice cores: relevance for future climate change, Clim. Past, 2, 145–165, https://doi.org/10.5194/cp-2-145-2006, 2006. a
Masson-Delmotte, V., Hou, S., Ekaykin, A., Jouzel, J., Aristarain, A., Bernardo, R. T., Bromwich, D., Cattani, O., Delmotte, M. M., Falourd, S., Frezzotti, M., Gallée, H., Genoni, L., Isaksson, E., Landais, A., Helsen, M. M., Hoffmann, G., Lopez, J., Morgan, V., Motoyama, H., Noone, D., Oerter, H., Petit, J. R., Royer, A., Uemura, R., Schmidt, G. A., Schlosser, E., Simões, J. C., Steig, E. J., Stenni, B., Stievenard, M., Van Den Broeke, M. R., Van De Wal, R. S., Van De Berg, W. J., Vimeux, F., and White, J. W.: A review of antarctic surface snow isotopic composition: Observations, atmospheric circulation, and isotopic modeling, J. Climate, 21, 3359–3387, https://doi.org/10.1175/2007JCLI2139.1, 2008. a, b
Matsikaris, A., Widmann, M., and Jungclaus, J.: On-line and off-line data assimilation in palaeoclimatology: a case study, Clim. Past, 11, 81–93, https://doi.org/10.5194/cp-11-81-2015, 2015. a, b
Münch, T., Kipfstuhl, S., Freitag, J., Meyer, H., and Laepple, T.: Constraints on post-depositional isotope modifications in East Antarctic firn from analysing temporal changes of isotope profiles, The Cryosphere, 11, 2175–2188, https://doi.org/10.5194/tc-11-2175-2017, 2017. a
Nicolas, J. P. and Bromwich, D. H.: New reconstruction of antarctic near-surface temperatures: Multidecadal trends and reliability of global reanalyses, J. Climate, 27, 8070–8093, https://doi.org/10.1175/JCLI-D-13-00733.1, 2014. a, b, c, d, e, f, g, h, i, j, k
Orsi, A. J., Cornuelle, B. D., and Severinghaus, J. P.: Little Ice Age cold interval in West Antarctica: Evidence from borehole temperature at the West Antarctic Ice Sheet (WAIS) Divide, Geophys. Res. Lett., 39, 1–7, https://doi.org/10.1029/2012GL051260, 2012. a, b
Otto-Bliesner, B. L., Joussaume, S., Braconnot, P., Harrison, S. P., and Abe-Ouchi, A.: Modeling and Data Syntheses of Past Climates: Paleoclimate Modelling Intercomparison Project Phase II Workshop, Estes Park, Colorado, 15–19 September 2008, Eos T. Am. Geophys. Un., 90, p. 93, https://doi.org/10.1029/2009EO110013, 2009. a, b
Otto-Bliesner, B. L., Brady, E. C., Fasullo, J., Jahn, A., Landrum, L., Stevenson, S., Rosenbloom, N., Mai, A., and Strand, G.: Climate variability and change since 850 ce an ensemble approach with the community earth system model, B. Am. Meteorol. Soc., 97, 787–801, https://doi.org/10.1175/BAMS-D-14-00233.1, 2016. a
PAGES 2k-PMIP3 group: Continental-scale temperature variability in PMIP3 simulations and PAGES 2k regional temperature reconstructions over the past millennium, Clim. Past, 11, 1673–1699, https://doi.org/10.5194/cp-11-1673-2015, 2015. a, b
PAGES 2k Consortium: Continental-scale temperature variability during the past two millennia, Nat. Geosci., 6, 339–346, https://doi.org/10.1038/ngeo1797, 2013. a, b, c, d
Pendergrass, A. G., Hakim, G. J., Battisti, D. S., and Roe, G.: Coupled air-mixed layer temperature predictability for climate reconstruction, J. Climate, 25, 459–472, https://doi.org/10.1175/2011JCLI4094.1, 2012. a
Rayner, N. A., Parker, D., Horton, E., Folland, C., Alexander, L., Rowell, D., Kent, E., and Kaplan, A.: Global analyses of sea surface temperature, sea ice, and night marine air temperature since the late nineteenth century, J. Geophys. Res., 108, 4407, https://doi.org/10.1029/2002JD002670, 2003. a
Ritter, F., Steen-Larsen, H. C., Werner, M., Masson-Delmotte, V., Orsi, A., Behrens, M., Birnbaum, G., Freitag, J., Risi, C., and Kipfstuhl, S.: Isotopic exchange on the diurnal scale between near-surface snow and lower atmospheric water vapor at Kohnen station, East Antarctica, The Cryosphere, 10, 1647–1663, https://doi.org/10.5194/tc-10-1647-2016, 2016. a
Roche, D. M.: δ18O water isotope in the iLOVECLIM model (version 1.0) – Part 1: Implementation and verification, Geosci. Model Dev., 6, 1481–1491, https://doi.org/10.5194/gmd-6-1481-2013, 2013. a
Schlosser, E., Reijmer, C., Oerter, H., and Graf, W.: The influence of precipitation origin on the delta(18)O-T relationship at Neumayer station, Ekstromisen, Antarctica, Ann. Glaciol., 39, 41–48, https://doi.org/10.3189/172756404781814276, 2004. a
Schmidt, G. A., Jungclaus, J. H., Ammann, C. M., Bard, E., Braconnot, P., Crowley, T. J., Delaygue, G., Joos, F., Krivova, N. A., Muscheler, R., Otto-Bliesner, B. L., Pongratz, J., Shindell, D. T., Solanki, S. K., Steinhilber, F., and Vieira, L. E. A.: Climate forcing reconstructions for use in PMIP simulations of the last millennium (v1.0), Geosci. Model Dev., 4, 33–45, https://doi.org/10.5194/gmd-4-33-2011, 2011. a
Schmidt, G. A., Kelley, M., Nazarenko, L., Ruedy, R., Russell, G. L., Aleinov, I., Bauer, M., Bauer, S. E., Bhat, M. K., Bleck, R., Canuto, V., Chen, Y.-h., Cheng, Y., Clune, T. L., Genio, A. D., Fainchtein, R. D., Faluvegi, G., Hansen, J. E., Healy, R. J., Kiang, N. Y., Koch, D., Lacis, A. a., Legrande, A. N., Lerner, J., Lo, K. K., Matthews, E. E., Menon, S., Miller, R. L., Oinas, V., Oloso, A. O., Perlwitz, J. P., Puma, M. J., Putman, W. M., Rund, D., Romanou, A., Sato, M., Shindell, D. T., Sun, S., Syed, R. A., Tausnev, N., Tsigaridis, K., Unger, N., Voulgarakis, A., Yao, M.-S., and Zhang, J.: Configuration and assessment of the GISS ModelE2 contributions to the CMIP5 archive, J. Adv. Model. Earth Sy., 6, 141–184, https://doi.org/10.1002/2013MS000265, 2014. a
Schneider, D. P., Steig, E. J., Van Ommen, T. D., Dixon, D. A., Mayewski, P. A., Jones, J. M., and Bitz, C. M.: Antarctic temperatures over the past two centuries from ice cores, Geophys. Res. Lett., 33, 1–5, https://doi.org/10.1029/2006GL027057, 2006. a, b
Sime, L. C., Tindall, J. C., Wolff, E. W., Connolley, W. M., and Valdes, P. J.: Antarctic isotopic thermometer during a CO2 forced warming event, J. Geophys. Res.-Atmos., 113, 1–16, https://doi.org/10.1029/2008JD010395, 2008. a, b
Sjolte, J., Sturm, C., Adolphi, F., Vinther, B. M., Werner, M., Lohmann, G., and Muscheler, R.: Solar and volcanic forcing of North Atlantic climate inferred from a process-based reconstruction, Clim. Past, 14, 1179–1194, https://doi.org/10.5194/cp-14-1179-2018, 2018. a, b, c, d
Smerdon, J. E.: Climate models as a test bed for climate reconstruction methods: Pseudoproxy experiments, WIRES Clim. Change, 3, 63–77, https://doi.org/10.1002/wcc.149, 2012. a, b
Smerdon, J. E., Coats, S., and Ault, T. R.: Model-dependent spatial skill in pseudoproxy experiments testing climate field reconstruction methods for the Common Era, Clim. Dynam., 46, 1921–1942, https://doi.org/10.1007/s00382-015-2684-0, 2016. a, b
Smith, K. L. and Polvani, L. M.: Spatial patterns of recent Antarctic surface temperature trends and the importance of natural variability: lessons from multiple reconstructions and the CMIP5 models, Clim. Dynam., 48, 2653–2670, https://doi.org/10.1007/s00382-016-3230-4, 2017. a
Sodemann, H. and Stohl, A.: Asymmetries in the moisture origin of Antarctic precipitation, Geophys. Res. Lett., 36, 1–5, https://doi.org/10.1029/2009GL040242, 2009. a
Steiger, N. J.: Historical climate model output of ECHAM5-wiso from 1871–2011 at T106 resolution, Data set, Zenodo, https://doi.org/10.5281/zenodo.1249604, 2018. a
Steiger, N. J., Hakim, G. J., Steig, E. J., Battisti, D. S., and Roe, G. H.: Assimilation of time-averaged pseudoproxies for climate reconstruction, J. Climate, 27, 426–441, https://doi.org/10.1175/JCLI-D-12-00693.1, 2014. a, b, c
Steiger, N. J., Steig, E. J., Dee, S. G., Roe, G. H., and Hakim, G. J.: Climate reconstruction using data assimilation of water isotope ratios from ice cores, J. Geophys. Res.-Atmos., 122, 1545–1568, https://doi.org/10.1002/2016JD026011, 2017. a, b, c, d, e, f
Steiger, N. J., Smerdon, J. E., Cook, E. R., and Cook, B. I.: A reconstruction of global hydroclimate and dynamical variables over the Common Era, Scientific Data, 5, 1–15, https://doi.org/10.1038/sdata.2018.86, 2018. a, b
Stenni, B., Curran, M. A. J., Abram, N. J., Orsi, A., Goursaud, S., Masson-Delmotte, V., Neukom, R., Goosse, H., Divine, D., van Ommen, T., Steig, E. J., Dixon, D. A., Thomas, E. R., Bertler, N. A. N., Isaksson, E., Ekaykin, A., Werner, M., and Frezzotti, M.: Antarctic climate variability on regional and continental scales over the last 2000 years, Clim. Past, 13, 1609–1634, https://doi.org/10.5194/cp-13-1609-2017, 2017. a, b, c, d, e, f, g, h, i, j, k, l, m, n, o, p, q, r, s, t, u, v, w, x, y, z, aa, ab, ac, ad, ae, af, ag, ah, ai, aj, ak, al, am, an, ao, ap
Stevens, B., Giorgetta, M., Esch, M., Mauritsen, T., Crueger, T., Rast, S., Salzmann, M., Schmidt, H., Bader, J., Block, K., Brokopf, R., Fast, I., Kinne, S., Kornblueh, L., Lohmann, U., Pincus, R., Reichler, T., and Roeckner, E.: The atmospheric component of the MPI-M earth system model: ECHAM6, J. Adv. Model. Earth Sy., 5, 1–27, https://doi.org/10.1002/jame.20015, 2013. a
Taylor, K. E., Stouffer, R. J., and Meehl, G. A.: An Overview of CMIP5 and the Experiment Design, B. Am. Meteorol. Soc., 93, 485–498, https://doi.org/10.1175/BAMS-D-11-00094.1, 2012. a, b, c
van Leeuwen, P. J.: Particle Filtering in Geophysical Systems, Mon. Weather Rev., 137, 4089–4114, https://doi.org/10.1175/2009MWR2835.1, 2009. a
Wang, J., Emile-Geay, J., Guillot, D., Smerdon, J. E., and Rajaratnam, B.: Evaluating climate field reconstruction techniques using improved emulations of real-world conditions, Clim. Past, 10, 1–19, https://doi.org/10.5194/cp-10-1-2014, 2014. a
Werner, M., Langebroek, P. M., Carlsen, T., Herold, M., and Lohmann, G.: Stable water isotopes in the ECHAM5 general circulation model: Toward high-resolution isotope modeling on a global scale, J. Geophys. Res.-Atmos., 116, 1–14, https://doi.org/10.1029/2011JD015681, 2011. a, b, c, d
Werner, M., Haese, B., Xu, X., Zhang, X., Butzin, M., and Lohmann, G.: Glacial-interglacial changes in H218O, HDO and deuterium excess – results from the fully coupled ECHAM5/MPI-OM Earth system model, Geosci. Model Dev., 9, 647–670, https://doi.org/10.5194/gmd-9-647-2016, 2016. a, b, c, d, e, f
Widmann, M., Goosse, H., van der Schrier, G., Schnur, R., and Barkmeijer, J.: Using data assimilation to study extratropical Northern Hemisphere climate over the last millennium, Clim. Past, 6, 627–644, https://doi.org/10.5194/cp-6-627-2010, 2010. a
Wu, T., Song, L., Li, W., Wang, Z., Zhang, H., Xin, X., Zhang, Y., Zhang, L., Li, J., Wu, F., Liu, Y., Zhang, F., Shi, X., Chu, M., Zhang, J., Fang, Y., Wang, F., Lu, Y., Liu, X., Wei, M., Liu, Q., Zhou, W., Dong, M., Zhao, Q., Ji, J., Li, L., and Zhou, M.: An overview of BCC climate system model development and application for climate change studies, J. Meteorol. Res., 28, 34–56, 2014. a
- Abstract
- Introduction
- Data and methods
- Reconstructed and simulated last millennium temperature changes
- Potential for reconstructing surface temperature based on water stable isotopes
- Reconstructions based on real δ18O data
- Conclusions
- Data availability
- Competing interests
- Acknowledgements
- Review statement
- References
- Supplement
- Abstract
- Introduction
- Data and methods
- Reconstructed and simulated last millennium temperature changes
- Potential for reconstructing surface temperature based on water stable isotopes
- Reconstructions based on real δ18O data
- Conclusions
- Data availability
- Competing interests
- Acknowledgements
- Review statement
- References
- Supplement