the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Experimental evaluation of oxygen isotopic exchange between inclusion water and host calcite in speleothems
Yudai Kina
Chuan-Chou Shen
Kanako Omine
The oxygen and hydrogen isotopic compositions of water in fluid inclusions in speleothems are important hydroclimate proxies because they provide information on the isotopic compositions of rainwater in the past. Moreover, because isotopic differences between fluid inclusion water and the host calcite provide information on the past isotopic fractionation factor, they are also useful for quantitative estimation of past temperature changes. The oxygen isotope ratio of inclusion water (δ18Ofi), however, may be affected by isotopic exchange between the water and the host carbonate. Thus, it is necessary to estimate the bias caused by this postdepositional effect for precise reconstruction of paleotemperatures. Here, we evaluate the isotopic exchange reaction between inclusion water and host calcite based on a laboratory experiment involving a natural stalagmite. Multiple stalagmite samples cut from the same depth interval were heated at 105 ∘C in the laboratory from 0 to 80 h. Then, the isotopic compositions of the inclusion water were measured. In the 105 ∘C heating experiments, the δ18Ofi values increased from the initial value by 0.7 ‰ and then remained stable after ca. 20 h. The hydrogen isotope ratio of water showed no trend in response to the heating experiments, suggesting that the hydrogen isotopic composition of fluid inclusion water effectively reflects the composition of past drip water. We then evaluated the process behind the observed isotopic variations using a partial equilibration model. The experimental results are best explained by the assumption that a thin CaCO3 layer surrounding the inclusion reacted with the water. The amount of CaCO3 that reacted with the water is equivalent to 2 % of the water inclusions in molar terms. These results suggest that the magnitude of the isotopic exchange effect has a minor influence on paleotemperature estimates for Quaternary climate reconstructions.
Speleothems have provided invaluable terrestrial climate records over historical (e.g., Zhang et al., 2008) and glacial–interglacial (e.g., Wang, 2001; Wang et al., 2017) timescales. Among multiple climate proxies in speleothems (Fairchild et al., 2006), the stable oxygen isotope ratio of CaCO3 (δ18Oca) is the most widely used hydroclimate proxy. Changes in δ18Oca have been interpreted as proxies for monsoon strength (Wang, 2001), precipitation amount (Wang et al., 2017) or temperature (Dorale, 1998; Mori et al., 2018), depending on the hydroclimatic setting of each cave site.
The indeterminate nature of δ18Oca interpretation is related to the fact that the δ18Oca values are mainly controlled by two factors: the temperature in the cave and the annual mean δ18O value of the rainwater. To overcome this ambiguity, the isotopic compositions of water in fluid inclusions in stalagmites have been regarded as important proxies (Schwarcz et al., 1976; McDermott, 2004). Cave drip waters are sealed in microscale cavities as fluid inclusions, whose δ18O value is usually close to the δ18O value of the infiltration-weighted mean of local rain (Baker et al., 2019). Generally, stalagmites contain inclusion water, which accounts for 0.05 wt % to 0.5 wt % of a speleothem (McDermott, 2005). Thus, the isotopic compositions of fluid inclusions in stalagmites (δ18Ofi) trapped under humid conditions should directly preserve the δ18O value of drip water in the past.
δ18Ofi values are also useful for estimating past temperature variations. Although experimental studies suggest that the δ18Oca values of speleothems are affected by kinetic effects (e.g., Hansen et al., 2019; Dietzel et al., 2009), a modeling study suggests the temperature dependence of δ18Oca is within the range of −0.20 ‰ ∘C−1 and −0.34 ‰ ∘C−1 even under a kinetic condition (Mühlinghaus et al., 2009). The combination of the two isotopic compositions, δ18Ofi and δ18Oca, provides a direct estimate for the oxygen isotopic fractionation between calcite and water, which is controlled mainly by the formation temperature. Thus, variations in past temperature (i.e., not absolute values but relative changes) can be estimated on the assumption that the kinetic effect is constant during the speleothem formation period.
Early studies analyzed the hydrogen isotope ratio of fluid inclusion water (δDfi), and the δ18Ofi value was inferred from the modern δD vs. δ18O relation in meteoric water (Schwarcz et al., 1976; Harmon et al., 1979; Genty et al., 2002; Matthews et al., 2000; and McGarry et al., 2004). These studies measured δDfi because of the technical difficulties associated with measuring the small amounts required to estimate δ18Ofi values and a fundamental concern about the integrity of the δ18Ofi data, namely, oxygen isotopic exchange between inclusion water and host calcite in speleothems.
After being trapped in the host calcite, inclusion water may continue to exchange oxygen isotopes with the surrounding host calcite as follows:
This isotopic re-equilibration effect potentially alters δ18Ofi values after the initial trapping of the inclusion water in the stalagmite. Such postdepositional isotopic exchange does not occur for hydrogen because of the small amount of hydrogen in the host calcite. Many studies on geothermal water have shown positive δ18O shifts from the global meteoric water line (GMWL) (Clark and Fritz, 1999, and references therein). These data suggest an isotopic exchange of oxygen between the geothermal water and the host aquifer rocks. This observation is one of the reasons why the earlier studies mentioned above explored δD values of fluid inclusions rather than δ18Ofi values (Harmon et al., 1979; Matthews et al., 2000; McGarry et al., 2004).
Recently, because of technological developments involving continuous-flow isotope ratio mass spectrometry (Vonhof et al., 2006) and cavity ring-down spectrometry (CRDS) (Uemura et al., 2016; Arienzo et al., 2013; Affolter et al., 2014), isotopic data from fluid inclusion have been accumulating. Interestingly, these studies suggest that postdepositional exchange is not significant. In fact, the fluid inclusions analyses of modern stalagmites have shown that their δ18Ofi values are consistent with the δ18O values of modern drip waters (Griffiths et al., 2010; Dennis et al., 2001; Arienzo et al., 2013; Uemura et al., 2016; Labuhn et al., 2015), although a postdepositional alternation induced by recrystallization has been suggested (Demény et al., 2016). Moreover, several studies successfully quantitatively estimated past temperatures at the time of calcite formation (van Breukelen et al., 2008; Meckler et al., 2015; Uemura et al., 2016). Therefore, these data imply that the oxygen isotopic exchange between inclusion water and stalagmite calcite appears to be limited and/or very slow over natural temperature ranges.
The indirect evidence for the insignificant postdepositional effect cannot provide explanations for the mechanisms behind this phenomenon. Thus, it is essential to investigate the isotopic exchange reaction and evaluate how much the past temperature reconstruction would be biased by this effect. However, to our knowledge, no study has investigated the magnitude of isotopic exchange within natural stalagmites. In addition to this natural process, the isotopic exchange reaction may occur during the drying process of stalagmite samples at high temperatures, which was commonly conducted before fluid inclusion measurement in the laboratory (Affolter et al., 2014; Vonhof et al., 2006; Uemura et al., 2016; Dublyansky and Spötl, 2009).
Here, we evaluate the isotopic exchange reaction between inclusion water and host calcite based on a laboratory heating experiment of natural stalagmite samples. We conducted a heating experiment because a higher temperature induces an increase in the degree of isotopic disequilibrium between water and calcite and increases the rate of isotopic exchange. As a result, an isotopic shift caused by the exchange reaction will be easier to detect. The stalagmite samples and experimental settings are described in Sect. 2. Section 3 presents the experimental results and discusses them using an isotopic exchange model for inclusion water and host calcite. Concluding remarks are given in Sect. 4.
2.1 Speleothem and drip water samples
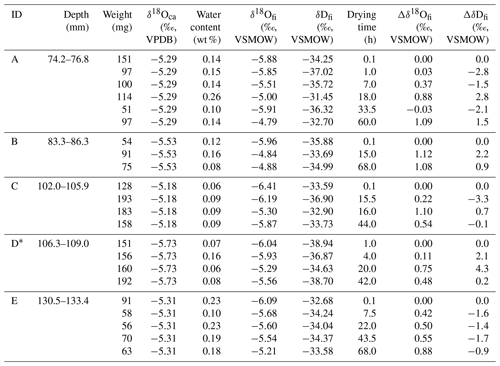
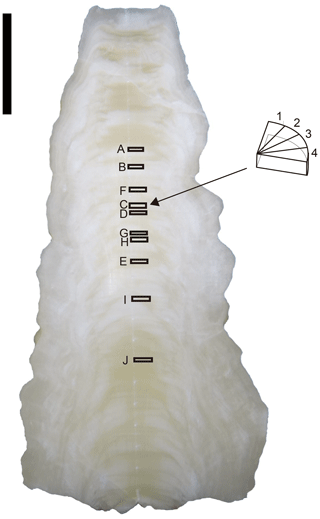
A stalagmite (named HSN1) was collected in Hoshino Cave, Minami-Daito Island, Okinawa, Japan (25∘51′34′′ N, 131∘13′29′′ E). The stalagmite is 246 mm in length, and most parts are milky white with thin transparent layers (Fig. 1). The fabric of the milky white layer is an open columnar structure. To compare the isotope ratios of fluid inclusions after different heating times, 10 layers, A–J, were taken (2.4–3.9 mm in thickness) from a quartered section of the stalagmite (Tables 1 and 2). The position relative to the axis may have an influence on the water content. Thus, to minimize this effect, three to six wedge-shaped chipped subsamples (51–193 mg) were cut from each layer (illustrated in Fig. 1). Subsamples from the same depth interval were assumed to have the same isotopic compositions.
Drip water samples were collected in Hoshino Cave from March 2011 to May 2016 (one to five times per year). At present, there is no drip water at the sampling point of HSN1; the drip water samples were collected at a point ca. 50 m away from the sampling point.
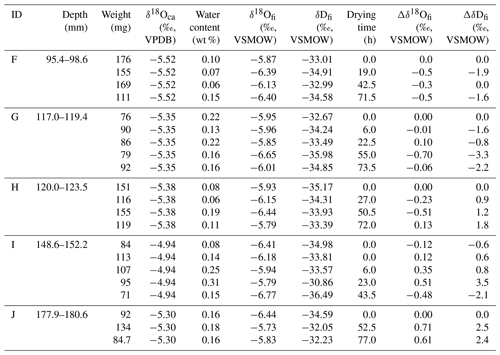
Table 2Isotopic compositions of inclusion waters and calcite in the HSN1 stalagmite for the 25 ∘C experiment.
2.2 Isotope measurements
The oxygen and hydrogen isotopic compositions of the water in the fluid inclusions were measured using a homemade extraction device (Uemura et al., 2016). Briefly, the speleothem sample was crushed under vacuum, and then extracted water vapor was transferred to a CRDS isotope ratio analyzer (L2130-i, Picarro Inc.) at the University of the Ryukyus. Compared with the system described in Uemura et al. (2016), the system has been improved in the following three ways: (1) the valves were automatically controlled using pneumatic valves; (2) the entire system was heated at 105 ∘C, because most parts were easily damaged at 150 ∘C; and (3) the water vapor extracted from the stalagmite was immediately trapped cryogenically at the temperature of liquid nitrogen, thereby preventing interaction between CaCO3 and water vapor. The 1σ reproducibility for the inclusion water analysis, based on the replicate analyses, was ±0.3 ‰ for δ18O and ±1.6 ‰ for δD (Uemura et al., 2016).
The δ18O and δD values were measured simultaneously using a cavity ring-down spectrometer (L2130-i, Picarro Inc.) with a vaporizer unit (V1120-i, Picarro Inc.). The 1σ reproducibility, based on repeated analyses of a working standard water, was ±0.08 ‰ for δ18O and ±0.26 ‰ for δD.
Stalagmite carbonate subsamples were measured using an isotope ratio mass spectrometer (Thermo Scientific DELTA V Advantage) equipped with a Thermo Scientific GasBench II system at the University of the Ryukyus. Powdered subsamples of 150–200 µg were reacted with 100 % phosphoric acid at 72 ∘C in septa-capped vials before measuring the released CO2. The 1σ (n=124) reproducibility for the analysis was ±0.04 ‰ for δ18O and ±0.03 ‰ for δ13C, based on repeated analyses of a carbonate standard (IAEA-CO-1).
The isotopic composition is expressed in units of per mill (‰) using delta notation (), where R is the isotopic ratio and Rsample and Rref are the isotopic ratios of the sample and reference, respectively. For water samples from fluid inclusions, δ18O and δD data are presented relative to Vienna Standard Mean Ocean Water (VSMOW) and are normalized to the VSMOW–SLAP scale. For calcite samples, δ18O and δ13C data are expressed relative to the Vienna Pee Dee Belemnite (VPDB) and/or VSMOW references. For clarity, δ values for fluid inclusion water and stalagmite calcite are expressed with the subscripts “fi” and “ca”, respectively. δ18Ofi, for example, indicates the δ18O value of the water in fluid inclusions.
Two layers (depths of 75.0 and 190.0 mm) of the HSN1 stalagmite were dated using U–Th techniques (Shen et al., 2008, 2012). U–Th isotopic compositions and concentrations were measured on a multicollector inductively coupled plasma mass spectrometer (Neptune, Thermo Fisher Scientific Inc.) at the High-Precision Mass Spectrometry and Environment Change Laboratory (HISPEC) of the Department of Geosciences at National Taiwan University (Shen et al., 2012). U–Th ages were calculated based on decay constants, half-lives and 238U∕235U ratios (Jaffey et al., 1971; Cheng et al., 2013; Hiess et al., 2012). Uncertainties in the U–Th isotopic data and 230Th dates (yr BP, before 1950 CE) are given at the two-sigma (2σ) level or 2 standard deviations of the mean (2σm) unless otherwise noted.
2.3 Heating experiment
To evaluate the effect of isotopic exchange between water and host calcite, a heating experiment was conducted. As a pretreatment process, each stalagmite sample was placed in a small glass tube (o.d. 0.5 in. and 6 cm in length) with an airtight screw cap sealed with two Viton O-rings. Then, the samples were dried in a vacuum line for 17 h at room temperature using a turbo molecular pump (with a pressure down to 10−5 Pa).
After this pre-drying process for all samples, the sample tube was subjected to different temperatures of 105 or 25 ∘C. For the 105 ∘C heating experiment, the sample tube was heated with a silicone cable heater at 105 ∘C for a defined time period (from 0 to 70 h) under the same vacuum conditions (i.e., a pressure down to 10−5 Pa). For comparison, we also performed a non-heating experiment at room temperature (25 ∘C) for the same time periods (from 0 to 70 h) under the same vacuum conditions.
Then, the heated (or non-heated) sample was transferred in the closed sample tube to the fluid inclusion analysis apparatus so that atmospheric exposure when introducing the sample lasted for less than 30 s. To evacuate the analytical line, the samples were subjected to an additional 105 ∘C condition for 20 min. Then, the sample was crushed, and the isotopic composition of the inclusion water was measured as described in Sect. 2.2.
3.1 Isotope composition of inclusion water
The temporal variations in δ18Ofi and δDfi values resulting from the 105 ∘C heating and non-heating experiments are shown in Fig. 2. The isotopic compositions of inclusion water are shown as a deviation from the initial value (Δδ18Ofi and ΔδDfi). For the 105 ∘C heating experiment, the δ18Ofi values gradually increased with the heating time and then reached a constant value after ca. 20 h (Fig. 2a). The regression curve of the data represents an exponential function (Sect. 3.5). The δ18Ofi values increased by ca. 0.7 ‰ with respect to the initial values during ca. 20 h from the start of heating (Fig. 2a). In contrast, no significant trend was found for ΔδDfi in the 105 ∘C heating experiment (Fig. 2b). For the room-temperature drying experiment, neither Δδ18Ofi nor ΔδDfi values showed any systematic variation (Fig. 2c and d).
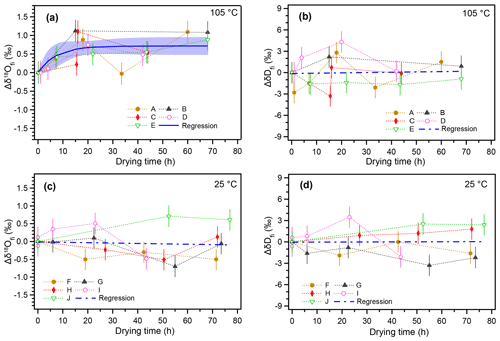
Figure 2Changes in isotopic compositions of inclusion water with increasing drying time. (a) Changes in the δ18O value of inclusion water from the initial value () with time under 105 ∘C heating. Time on the x axis indicates drying time in addition to the standard 17 h drying process at room temperature. (b) The same as (a) but for δDfi. (c) Changes in the value over time at room temperature (25 ∘C). (d) The same as (c) but for δDfi. The error bar of the data point represents the analytical reproducibility (1σ). The regression curve (blue) in panel (a) was calculated with IGOR (WaveMetrics Inc.) software to fit a function () (A=0.71: k=0.14). The blue shade indicates the 95 % confidence interval. Blue dashed lines in panels (b)–(d) indicate linear regression lines (the correlations are insignificant).
Overall, the results suggest that the observed increase in δ18Ofi values in the 105 ∘C heating experiment is caused by the oxygen isotopic exchange between inclusion water and the surrounding calcite. The data from the control experiment at room temperature suggest that the oxygen isotopic exchange reaction is too small to detect under 25 ∘C conditions. The δDfi data for the 25 ∘C experiment confirm that there is no systematic isotopic variation caused by subsample cutting and length of drying time. In addition, the ΔδDfi value for the 105 ∘C experiment did not change because there is no significant hydrogen reservoir in calcite.
The new calcite precipitation in fluid inclusions did not occur because the δ18Ofi is expected to be lower if the new calcite, whose δ18O value is higher than that of water, formed inside the inclusions. This is opposite to the heating experiment result. In the case of internal calcite dissolution, the δ18O value of water will be changed through the isotopic exchange reaction between the bicarbonate in the solution and the water. Thus, if the amount of dissolution is limited, it is not different from the case in which the water is re-equilibrated with a limited amount of CaCO3 (this will be discussed in Sect. 3.4).
3.2 Evaporation during heating
Long-term heating may induce leakage from water inclusions through microscopic channels in the calcite caused by decrepitation of the calcite. The measured water content (weight ratio of water in fluid inclusions to carbonate) of the experiments is shown in Fig. 3. Overall, the water content ranged from 0.05 wt % to 0.3 wt %, which is within the typical observed range of 0.05 %–0.5 % (McDermott, 2005).
Although there are large variations in water content among different layers, there is no significant trend between heating time and water content (Fig. 3). This result suggests that the fluid inclusion water does not evaporate/leak even after long-term heating. We should note that larger data sets of various stalagmites are needed to generalize this result because the behavior of leakage would also be influenced by the fabric and microstructure of the stalagmite. In addition, this finding suggests that our standard drying procedure (17 h at room temperature, as described in Methods) is enough to remove the water adsorbed onto the calcite. Therefore, this result confirms that the increase in δ18Ofi values (Fig. 2a) in the heating experiments is not caused by evaporation due to thermal decrepitation.
3.3 Evidence of a postdepositional effect in the D–O plot
The distinct behavior of δDfi and δ18Ofi values is clearly depicted in the δD–δ18O plot (Fig. 4). The GMWL, local meteoric water line (LMWL) and precipitation-weighted annual mean values (2009–2012) of the rainwater on Okinawa Island (also called Okinawa-jima) are shown in Fig. 4. The LMWLs for summer and winter seasons are calculated based on the rainwater data from Okinawa Island (Uemura et al., 2012), ca. 400 km west of Minami-Daito Island. The present-day drip water isotopic data of Hoshino Cave are close to the higher ones of annual mean precipitation values on Okinawa Island (Fig. 4). Generally, the initial δDfi and δ18Ofi values in the 25 ∘C experiment are scattered between the summer and winter LWMLs.
Table 3Thorium-230 dating results of stalagmite HSN1 from Hoshino Cave.

Chemical analyses were performed in March 2017. Analytical errors are 2σ of the mean. a (±0.65 ‰) (Hiess et al., 2012); δ234U . bδ234 Uinitial corrected was calculated based on 230Th age (T); i.e., δ234Uinitial=δ234U, and T is the corrected age. c [230Th∕238U] activity , where T is the age. The decay constants are 9.1705 yr−1 for 230Th, yr−1 for 234U and yr−1 for 238U. d The degree of detrital 230Th contamination is indicated by the [230Th∕232Th] atomic ratio instead of the activity ratio. e Age corrections for samples were calculated using an estimated atomic 230Th∕232Th ratio of 4±2 ppm. These are the values for a material at secular equilibrium, with a crustal 232Th∕238U of 3.8 and an arbitrary uncertainty of 50 %. BP indicates before present, where present is defined as 1950 CE.
The thorium-230 dating results of stalagmite HSN1 from Hoshino Cave are shown in Table 3. The ages of layers at depths of 75.0 and 190.0 mm were 6429±55 and 7092±48 years BP, respectively. Thus, a more detailed comparison between the HSN1 fluid inclusions and the present-day rainwater is not straightforward, because the HSN1 speleothem was grown during the mid-Holocene, and the rainwater isotope ratio is likely different from that of modern rainfall.
An important characteristic of this result is that the δ18Ofi values from the heating experiment are systematically shifted in the isotopically enriched direction. The average δ18Ofi value for the heating experiments ( ‰) is higher than that for the 25 ∘C experiment ( ‰) by 0.7 ‰. In contrast, the average value of δD does not differ between these experiments (9 ‰ in the heating experiment; ‰ in the room-temperature experiment).
Such a positive δ18O shift is opposite to the negative δ18O shift for inclusion water in speleothems possibly induced by recrystallization (Demény et al., 2016). Instead, the positive shift is similar to the δ18O shift from GMWL found in observations of geothermal water (Clark and Fritz, 1999). Although the magnitude of the shift is much larger for geothermal water, 5 ‰–15 ‰, the δ18Ofi shift found in our experiment is likely caused by the exchange of 18O between the inclusion water and the host calcite. The possible reasons for the small magnitude of the δ18O shift, 0.7 ‰, in our experiment will be discussed later (Sect. 3.4 and 3.5).

Figure 3Changes in water content with increasing drying time. Changes in water content (in wt %) of each subsample with time (in hours). Symbols indicate the 105 ∘C experiment (red, layer A–E) and 25 ∘C drying experiment (blue, layer F–J).
In fluid inclusion studies, closeness to the LMWL in δD–δ18O plots has been used as proof for the validity of analytical methods and the integrity of the sample. Our result calls for caution regarding the δD–δ18O plot test. Most of the inclusion data from the heating and room-temperature experiments are distributed between the summer and winter LWMLs. As discussed above, the artificial increase in the δ18O value by heating is systematic. However, it is difficult to detect such a shift in the δD–δ18O plot because the shift is small in the scattered data points. The data from the heating experiment (more than 10 h) plot outside the summer LMWL, but a 0.7 ‰ deviation could be interpreted as resulting from different climate conditions. Because the oxygen isotopic exchange results in higher δ18O values without a δD shift, the isotopic exchange results in a lower deuterium excess value (), a −6 ‰ shift in our experiment. We should note that the d value could become higher if the exchange takes place at lower temperatures than the original precipitation temperature. Therefore, the oxygen isotope exchange under changing temperatures may cause a slight deviation from the LMWL.
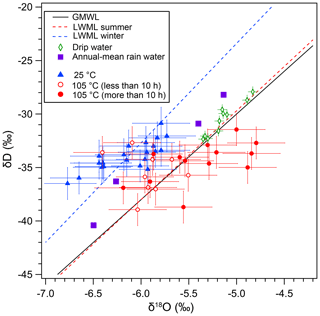
Figure 4D–O plot of inclusion water. Blue triangles indicate the isotopic compositions of the fluid inclusion in the 25 ∘C drying experiment. Red circles indicate the isotopic compositions of the fluid inclusion in the 105 ∘C drying experiment for < 10 h (open red circles) and > 10 h (solid red circles). The black line indicates GMWL. Local meteoric water lines based on present-day rain data from Okinawa Island for the summer season (red dotted line) and the winter season (blue dotted line) are also shown. Purple solid squares indicate precipitation-weighted annual mean values (2009–2012) of the rainwater on Okinawa Island. Green open diamonds indicate present-day observation of drip water in Hoshino Cave.
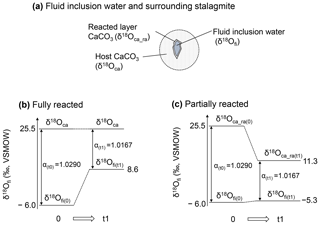
Figure 5Schematic illustration of isotopic re-equilibration between inclusion water and stalagmite. (a) Schematic illustration of a water-filled fluid inclusion and surrounding CaCO3. (b) Changes in the isotopic composition for the fully reacted hypothesis, in which the δ18Ofi value changes in response to equilibration with an infinite amount of host CaCO3. In this case, the sample at room temperature (25 ∘C at time of 0) is heated to 105 ∘C and reaches a new isotopic equilibrium at time t1. (c) The same as (b) but for the partially reacted hypothesis, in which the δ18Ofi value changes in response to equilibration with a limited amount of CaCO3. Note that the calcite–water fractionation factor is the same for both hypotheses.
3.4 Partial isotopic exchange between water and calcite
To interpret the experimental result, we consider two hypotheses: (i) the oxygen isotopic exchange reaction occurred between inclusion water and the entirety of the host calcite (hereafter referred to as the “fully reacted hypothesis”), and (ii) the δ18Ofi values are equilibrated with a limited amount of CaCO3 (hereafter referred to as the “partially reacted hypothesis”). These hypotheses are schematically explained in Fig. 5.
For the fully reacted hypothesis, the number of oxygen atoms in calcite can be considered infinite compared with those in the water inclusions because the water content of a stalagmite is very small, 0.05 wt %–0.5 wt % (McDermott, 2005). Thus, δ18Ofi is simply controlled by the δ18O value of calcite and the equilibrium fractionation factor between CaCO3 and H2O at the ambient temperature (Fig. 5b). At 105 ∘C, the fractionation factor between CaCO3 and water is 1.0167. Because the δ18Oca value of the HSN1 stalagmite is 25.5 ‰ vs. VSMOW (i.e., −5.3 ‰ vs. VPDB), the δ18Ofi value in equilibrium with the calcite should be 8.6 ‰ vs. VSMOW. Thus, the δ18Ofi value should be enriched by 14 ‰ to 15 ‰. This simple hypothesis, however, is not realistic because the inclusion water likely reacts only with the inner surface of CaCO3 surrounding the inclusions. In fact, the results in Fig. 2a show that the actual change in the δ18Ofi value is only 0.7 ‰.
The small δ18Ofi shift observed in the experiment can be interpreted as the result of (i) insufficient reaction time between water and calcite and/or (ii) reaction with a limited amount of CaCO3. The first hypothesis can be rejected because the Δδ18Ofi enrichment plateaued within 20 h (Fig. 2a). Therefore, the experimental results support the latter hypothesis. A model for this partially reacted hypothesis will be discussed in the following section.
3.5 Isotopic re-equilibration model
We describe a partial isotopic equilibration model that considers the changes in δ18Ofi values from the time when the inclusion water was entrapped in CaCO3 (time 0) to a certain time required to reach a new isotopic equilibrium (time t1; at a certain temperature T1). An example of this re-equilibration scenario is that inclusion waters at room temperature (time t=0, initial temperature is T0) are heated to 105 ∘C (T1) and reach a new isotope equilibrium at time t1.
For the partially reacted hypothesis, we assumed that a limited amount of CaCO3 in the reacted layer exchanged oxygen isotopes with the inclusion water (Fig. 5a). The isotope mass balance between the initial and partially equilibrated conditions at a heating time during a course of reaction at time t can be written as follows:
where γ is the molar ratio of CaCO3 involved in the reaction to the inclusion water (i.e., γ= CaCO3 in reacted layer/H2O in inclusion: /), indicates the δ18O value of the CaCO3 in the reacted layer and indicates the δ18O value of the inclusion water at time t. If the CaCO3 does not react with the water (i.e., γ=0), for example, the δ18Ofi value does not change before and after the reaction.
At t1, and reach an isotopic equilibrium state. This equilibrium state can be written as follows:
where indicates the oxygen isotopic enrichment factor at the temperature T1. Whereas the rate constant of the isotope exchange reaction only varies with temperature, the number of transferred isotopes varies with the temporal evolution of the isotope ratios of the end-members. The reaction can be written as follows:
where () is the isotopic difference, is the isotopic enrichment factor at the new equilibrium state and k18 indicates a reaction constant. The integration of Eq. (4) yields
where () represents the oxygen isotopic enrichment factor at the initial temperature, T0.
To fit our experimental data, in which we measured the difference between heated and initial (i.e., non-heated) conditions, we took the difference between Eq. (5) and the initial condition (t=0) of Eq. (5) (). Thus, with Eq. (2), we obtain
where ) represents the δ18Ofi difference between the reacted and initial conditions. When the new equilibrium state is reached (t=t1), Eq. (6) yields
This equation provides an estimate of γ based on the experimental results.
A regression curve based on Eq. (5) is shown in Fig. 2a. Based on Eq. (7), the value of γ is estimated to be 0.02. This suggests that the amount of CaCO3 reacted with water is equivalent to 2 % of the water inclusions in molar terms. The thickness of the reacted layer of CaCO3 can be roughly estimated based on the assumption that the fluid inclusions filled with water are cubic with 50 µm edges. With a calcite density of 2.71 g cm−3, the thickness of the reacted layer of CaCO3 is estimated to be 0.6 µm.
This result is explained schematically in Fig. 5a and c. The δ18Ofi value increased by only 0.7 ‰. Since the equilibrium fractionation factor between CaCO3 and water at 105 ∘C is 1.0167, the δ18Oca of the reacted layer should be 11.3 ‰ vs. VSMOW. Thus, in this case, the δ18Oca value of the reacted layer changed significantly.
3.6 Impact for paleoclimate reconstruction
In this section, we estimate the impact of the isotopic exchange effect on Quaternary paleoclimate reconstructions. First, at 105 ∘C, detectable isotopic exchange occurred within 20 h. This finding suggests that researchers should be aware of this effect during experimental procedures, such as the heat drying process, before fluid inclusion measurements. Second, we consider a case in which the drip water enclosed in the fluid inclusions during a glacial period with a temperature of 15 ∘C re-equilibrates at the modern average temperature of 25 ∘C. The isotopic enrichment factors () for 15 and 25 ∘C are 30.6 ‰ and 28.4 ‰, respectively. Thus, based on Eq. (7) with a γ value of 0.02, the fluid inclusion oxygen isotope ratio δ18Ofi would increase by only 0.1 ‰. With the temperature dependence of the δ18O fractionation factor between water and calcite (0.2 ‰ ∘C−1), this isotopic exchange results in a 0.5 ∘C bias in the paleotemperature estimate. We should note that we do not know the reaction rate of the isotopic exchange under normal ambient temperatures. Calcite and fluid inclusion water might not reach a new equilibrium state even after thousands of years. Thus, this estimate is an upper limit of the bias. Because the bias, 0.1 ‰, is within the typical analytical error for inclusion analyses, the postdepositional effect has little influence on the paleotemperature estimates for glacial–interglacial cycles.
Our experiment shows that δ18O values of fluid inclusion water in speleothems change because of isotopic exchange reactions with the host calcite. Unlike the δ18O value of inclusion water, the δD value showed no trend even after prolonged heating and thus effectively reflects the original isotopic composition of past drip water. This study is the first to present experimental data showing that such a postdepositional effect occurs in natural speleothem samples. However, the changes in the δ18O values of fluid inclusion water were very small, 0.7 ‰, in the 105 ∘C heating experiment. Based on this result, the inclusion water reacts only with a thin layer of surrounding CaCO3. The amount of CaCO3 that reacted with the water is equivalent to 2 % of the water inclusions in molar terms. Thus, the oxygen isotopic exchange results in a minor impact on the estimation of past temperature changes: a maximum bias of 0.5 ∘C for a 10 ∘C climate shift. This study provides a quantitative explanation of the mechanism by which the effect of isotopic exchange appears to be insignificant in previous speleothem studies. The results also suggest that the sample treatment in the laboratory (i.e., heated drying process) should be conducted with caution because isotopic exchange may affect the δ18O value of fluid inclusions.
The data generated and used in this study are available in Tables 1 and 2 in this article.
RU designed the experiment and study. YK and KO conducted the experiments. C-CS performed the U–Th dating. All authors contributed to the discussion. RU analyzed the results, generated figures and wrote the paper.
The authors declare that they have no conflict of interest.
We thank Eri Iwase, Satoru Mishima, Kosuke Masaka, Yuina Uechi, Tatsuki Matsuura, Masaaki Chinen (University of the Ryukyus) and Ryuji Asami (Tohoku University) for supporting the preparation and isotopic measurements and Tsai-Luen Yu for U–Th dating. We also thank Kazuaki Higashi for the assistance with field work.
This research has been supported by the Japan Society for the Promotion of Science (grant nos. 15H01729, 16H02235, 17KK0012, 18H03794). This study was also supported by the University of the Ryukyus Research Promotion Grant. U–Th dating was provided by grants from the Science Vanguard Research Program of the Ministry of Science and Technology (108-2119-M-002-012 to Chuan-Chou Shen) and the Higher Education Sprout Project of the Ministry of Education, Taiwan (108L901001 to Chuan-Chou Shen).
This paper was edited by Dominik Fleitmann and reviewed by two anonymous referees.
Affolter, S., Fleitmann, D., and Leuenberger, M.: New online method for water isotope analysis of speleothem fluid inclusions using laser absorption spectroscopy (WS-CRDS), Clim. Past, 10, 1291–1304, https://doi.org/10.5194/cp-10-1291-2014, 2014.
Arienzo, M. M., Swart, P. K., and Vonhof, H. B.: Measurement of δ18O and δ2H values of fluid inclusion water in speleothems using cavity ring-down spectroscopy compared with isotope ratio mass spectrometry, Rapid Commun. Mass Spectrom., 27, 2616–2624, https://doi.org/10.1002/rcm.6723, 2013.
Baker, A., Hartmann, A., Duan, W., Hankin, S., Comas-Bru, L., Cuthbert, M. O., Treble, P. C., Banner, J., Genty, D., Baldini, L. M., Bartolome, M., Moreno, A., Perez-Mejias, C., and Werner, M.: Global analysis reveals climatic controls on the oxygen isotope composition of cave drip water, Nat. Commun., 10, 2984, https://doi.org/10.1038/s41467-019-11027-w, 2019.
Cheng, H., Lawrence Edwards, R., Shen, C.-C., Polyak, V. J., Asmerom, Y., Woodhead, J., Hellstrom, J., Wang, Y., Kong, X., Spötl, C., Wang, X., and Calvin Alexander, E.: Improvements in 230Th dating, 230Th and 234U half-life values, and U–Th isotopic measurements by multi-collector inductively coupled plasma mass spectrometry, Earth Planet. Sc. Lett., 371–372, 82–91, https://doi.org/10.1016/j.epsl.2013.04.006, 2013.
Clark, I. and Fritz, P.: Water-Rock Interaction, in: Environmental Isotopes in Hydrogeology, Lewis Publishers, New York, 245–266, 1999.
Demény, A., Czuppon, G., Kern, Z., Leél-Őssy, S., Németh, A., Szabó, M., Tóth, M., Wu, C.-C., Shen, C.-C., Molnár, M., Németh, T., Németh, P., and Óvári, M.: Recrystallization-induced oxygen isotope changes in inclusion-hosted water of speleothems – Paleoclimatological implications, Quatern. Int., 415, 25–32, https://doi.org/10.1016/j.quaint.2015.11.137, 2016.
Dennis, P. F., Rowe, P. J., and Atkinson, T. C.: The recovery and isotopic measurement of water from fluid inclusions in speleothems, Geochim. Cosmochim. Ac., 65, 871–884, https://doi.org/10.1016/s0016-7037(00)00576-7, 2001.
Dietzel, M., Tang, J., Leis, A., and Köhler, S. J.: Oxygen isotopic fractionation during inorganic calcite precipitation – Effects of temperature, precipitation rate and pH, Chem. Geol., 268, 107–115, https://doi.org/10.1016/j.chemgeo.2009.07.015, 2009.
Dorale, J. A.: Climate and Vegetation History of the Midcontinent from 75 to 25 ka: A Speleothem Record from Crevice Cave, Missouri, USA, Science, 282, 1871–1874, https://doi.org/10.1126/science.282.5395.1871, 1998.
Dublyansky, Y. V. and Spötl, C.: Hydrogen and oxygen isotopes of water from inclusions in minerals: design of a new crushing system and on-line continuous-flow isotope ratio mass spectrometric analysis, Rapid Commun. Mass Spectrom., 23, 2605–2613, https://doi.org/10.1002/rcm.4155, 2009.
Fairchild, I. J., Smith, C. L., Baker, A., Fuller, L., Spötl, C., Mattey, D., McDermott, F., and EIMF: Modification and preservation of environmental signals in speleothems, Earth-Sci. Rev., 75, 105–153, https://doi.org/10.1016/j.earscirev.2005.08.003, 2006.
Genty, D., Plagnes, V., Causse, C., Cattani, O., Stievenard, M., Falourd, S., Blamart, D., Ouahdi, R., Van-Exter, S., and Caillon, N.: Fossil water in large stalagmite voids as a tool for paleoprecipitation stable isotope composition reconstitution and paleotemperature calculation, Chem. Geol., 184, 83–95, 2002.
Griffiths, M. L., Drysdale, R. N., Vonhof, H. B., Gagan, M. K., Zhao, J.-X., Ayliffe, L. K., Hantoro, W. S., Hellstrom, J. C., Cartwright, I., Frisia, S., and Suwargadi, B. W.: Younger Dryas–Holocene temperature and rainfall history of southern Indonesia from δ18O in speleothem calcite and fluid inclusions, Earth Planet. Sc. Lett., 295, 30–36, https://doi.org/10.1016/j.epsl.2010.03.018, 2010.
Hansen, M., Scholz, D., Schöne, B. R., and Spötl, C.: Simulating speleothem growth in the laboratory: Determination of the stable isotope fractionation (δ13C and δ18O) between H2O, DIC and CaCO3, Chem. Geol., 509, 20–44, https://doi.org/10.1016/j.chemgeo.2018.12.012, 2019.
Harmon, R. S., Schwarcz, H. P., and O'Neil, J. R.: D/H ratios in speleothem fluid inclusions: A guide to variations in the isotopic composition of meteoric precipitation?, Earth Planet. Sc. Lett., 42, 254–266, https://doi.org/10.1016/0012-821x(79)90033-5, 1979.
Hiess, J., Condon, D. J., McLean, N., and Noble, S. R.: 238U∕235U Systematics in Terrestrial Uranium-Bearing Minerals, Science, 335, 1610–1614, https://doi.org/10.1126/science.1215507, 2012.
Jaffey, A. H., Flynn, K. F., Glendenin, L. E., Bentley, W. C., and Essling, A. M.: Precision Measurement of Half-Lives and Specific Activities of 235U and 238U, Phys. Rev. C, 4, 1889–1906, https://doi.org/10.1103/PhysRevC.4.1889, 1971.
Labuhn, I., Genty, D., Vonhof, H., Bourdin, C., Blamart, D., Douville, E., Ruan, J., Cheng, H., Edwards, R. L., Pons-Branchu, E., and Pierre, M.: A high-resolution fluid inclusion δ18O record from a stalagmite in SW France: modern calibration and comparison with multiple proxies, Quaternary Sci. Rev., 110, 152–165, https://doi.org/10.1016/j.quascirev.2014.12.021, 2015.
Matthews, A., Ayalon, A., and Bar-Matthews, M.: D/H ratios of fluid inclusions of Soreq cave (Israel) speleothems as a guide to the Eastern Mediterranean Meteoric Line relationships in the last 120 ky, Chem. Geol., 166, 183–191, https://doi.org/10.1016/s0009-2541(99)00192-8, 2000.
McDermott, F.: Palaeo-climate reconstruction from stable isotope variations in speleothems: a review, Quaternary Sci. Rev., 23, 901–918, https://doi.org/10.1016/j.quascirev.2003.06.021, 2004.
McDermott, F., Schwarcz, H. P., and Rowe, P. J.: Isotopes in speleothems, in: Isotopes in Palaeoenvironmental Research, Springer, the Netherlands, Dordrecht, 185–226, 2005.
McGarry, S., Bar-Matthews, M., Matthews, A., Vaks, A., Schilman, B., and Ayalon, A.: Constraints on hydrological and paleotemperature variations in the Eastern Mediterranean region in the last 140ka given by the δD values of speleothem fluid inclusions, Quaternary Sci. Rev., 23, 919–934, https://doi.org/10.1016/j.quascirev.2003.06.020, 2004.
Meckler, A. N., Affolter, S., Dublyansky, Y. V., Krüger, Y., Vogel, N., Bernasconi, S. M., Frenz, M., Kipfer, R., Leuenberger, M., Spötl, C., Carolin, S., Cobb, K. M., Moerman, J., Adkins, J. F., and Fleitmann, D.: Glacial–interglacial temperature change in the tropical West Pacific: A comparison of stalagmite-based paleo-thermometers, Quaternary Sci. Rev., 127, 90–116, https://doi.org/10.1016/j.quascirev.2015.06.015, 2015.
Mori, T., Kashiwagi, K., Amekawa, S., Kato, H., Okumura, T., Takashima, C., Wu, C.-C., Shen, C.-C., Quade, J., and Kano, A.: Temperature and seawater isotopic controls on two stalagmite records since 83 ka from maritime Japan, Quaternary Sci. Rev., 192, 47–58, https://doi.org/10.1016/j.quascirev.2018.05.024, 2018.
Mühlinghaus, C., Scholz, D., and Mangini, A.: Modelling fractionation of stable isotopes in stalagmites, Geochim. Cosmochim. Ac., 73, 7275–7289, https://doi.org/10.1016/j.gca.2009.09.010, 2009.
Schwarcz, H. P., Harmon, R. S., Thompson, P., and Ford, D. C.: Stable isotope studies of fluid inclusions in speleothems and their paleoclimatic significance, Geochim. Cosmochim. Ac., 40, 657–665, https://doi.org/10.1016/0016-7037(76)90111-3, 1976.
Shen, C.-C., Li, K.-S., Sieh, K., Natawidjaja, D., Cheng, H., Wang, X., Edwards, R. L., Lam, D. D., Hsieh, Y.-T., Fan, T.-Y., Meltzner, A. J., Taylor, F. W., Quinn, T. M., Chiang, H.-W., and Kilbourne, K. H.: Variation of initial 230Th∕232Th and limits of high precision U–Th dating of shallow-water corals, Geochim. Cosmochim. Ac., 72, 4201–4223, https://doi.org/10.1016/j.gca.2008.06.011, 2008.
Shen, C.-C., Wu, C.-C., Cheng, H., Lawrence Edwards, R., Hsieh, Y.-T., Gallet, S., Chang, C.-C., Li, T.-Y., Lam, D. D., Kano, A., Hori, M., and Spötl, C.: High-precision and high-resolution carbonate 230Th dating by MC-ICP-MS with SEM protocols, Geochim. Cosmochim. Ac., 99, 71–86, https://doi.org/10.1016/j.gca.2012.09.018, 2012.
Uemura, R., Yonezawa, N., Yoshimura, K., Asami, R., Kadena, H., Yamada, K., and Yoshida, N.: Factors controlling isotopic composition of precipitation on Okinawa Island, Japan: Implications for paleoclimate reconstruction in the East Asian Monsoon region, J. Hydrol., 475, 314–322, https://doi.org/10.1016/j.jhydrol.2012.10.014, 2012.
Uemura, R., Nakamoto, M., Asami, R., Mishima, S., Gibo, M., Masaka, K., Jin-Ping, C., Wu, C.-C., Chang, Y.-W., and Shen, C.-C.: Precise oxygen and hydrogen isotope determination in nanoliter quantities of speleothem inclusion water by cavity ring-down spectroscopic techniques, Geochim. Cosmochim. Ac., 172, 159–176, https://doi.org/10.1016/j.gca.2015.09.017, 2016.
van Breukelen, M. R., Vonhof, H. B., Hellstrom, J. C., Wester, W. C. G., and Kroon, D.: Fossil dripwater in stalagmites reveals Holocene temperature and rainfall variation in Amazonia, Earth Planet. Sc. Lett., 275, 54–60, https://doi.org/10.1016/j.epsl.2008.07.060, 2008.
Vonhof, H. B., van Breukelen, M. R., Postma, O., Rowe, P. J., Atkinson, T. C., and Kroon, D.: A continuous-flow crushing device for on-line δ2H analysis of fluid inclusion water in speleothems, Rapid Commun. Mass Spectrom., 20, 2553–2558, https://doi.org/10.1002/rcm.2618, 2006.
Wang, X., Edwards, R. L., Auler, A. S., Cheng, H., Kong, X., Wang, Y., Cruz, F. W., Dorale, J. A., and Chiang, H.-W.: Hydroclimate changes across the Amazon lowlands over the past 45,000 years, Nature, 541, 204–207, https://doi.org/10.1038/nature20787, 2017.
Wang, Y. J.: A High-Resolution Absolute-Dated Late Pleistocene Monsoon Record from Hulu Cave, China, Science, 294, 2345–2348, https://doi.org/10.1126/science.1064618, 2001.
Zhang, P., Cheng, H., Edwards, R. L., Chen, F., Wang, Y., Yang, X., Liu, J., Tan, M., Wang, X., Liu, J., An, C., Dai, Z., Zhou, J., Zhang, D., Jia, J., Jin, L., and Johnson, K. R.: A Test of Climate, Sun, and Culture Relationships from an 1810-Year Chinese Cave Record, Science, 322, 940–942, https://doi.org/10.1126/science.1163965, 2008.